Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tri-five
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Tri-Five
Find all the DIFFERENT shapes that can be made by joining five equilateral triangles edge to edge.
Here's an example:
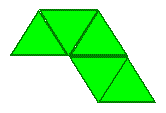
Why do this problem?
This activity is good for giving pupils the chance to explore shapes, order their solutions and create a system for getting all the solutions. It will provoke much discussion, encouraging learners to articulate their own ideas so providing a need to use appropriate vocabulary.
Possible approach
It would be good to have some time together using large equilateral triangles on the floor or table, with everyone gathered round. You could start by making a few examples as a whole group so that the aims are clear.
Give children time to explore other arrangements in pairs, using triangles cut from paper or card, or plastic shapes if you have them. If you do not have a large supply of these, you'll perhaps want to encourage pupils to record their arrangements in some way - isometric paper would be helpful.
Key questions
How are you checking that you have not got any of them twice?
Can you tell me about the way you're finding new arrangements?
Possible extension
What about getting pupils to ask "I wonder what would happen if we ...?"
Possible support
It would be a good idea to start with the Triangle Animals problem which involves making the different arrangements of three triangles.

