Watch your feet
Problem
Have you ever read a Winnie the Pooh poem called "Lines and Squares" by A.A. Milne? It tells us how Christopher Robin plays a game with himself as he walks along pavements, trying not to walk on the "lines" (the edges of the paving stones).
Have you ever done this? I know I have! This investigation is based on a similar idea - but here I want to walk on the lines!
This is a picture of the path leading up to my front door from the road:

I like to walk along the cracks of the paving stones, but not the outside edge of the path itself because I may tread on the grass.
The only way I can do it is by walking straight down the middle of the path like this:

If the path were three paving stones wide instead of just two it would look like this:

Remembering that I can only walk along the sides of the paving stones and I mustn't tread on the outside edge, how many different routes can you find for me to take? (By the way, you must not turn back on yourself, and you must head towards the door or sides - so you cannot walk towards the road on your journey.)
Do any of your routes have a repeating pattern?
Imagine now that the path is even wider, with four paving stones:

What different routes can you find now?
Perhaps you could group them into those with a repeating pattern and those without. Maybe you can find other ways to group the routes.
If I could also take steps diagonally across a paving stone, like this:

then there are even more possibilities. Try to find the new routes yourself, starting with 3 paving stones width. Remember all the same rules apply as before.
Getting Started
Student Solutions
We received some fantastic solutions to this Bernard's Bag investigation. One of these came from Adam, from Milton Mount School. Children at Summercroft Junior School who go to the lunchtime Challenge Club sent us some very interesting work: Laura B and Adam sent this diagram showing the longest possible route for a path 3 paving stones wide and 14 long:
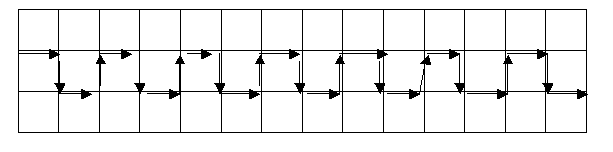
Along with Laura S, Eleanor and Oliver, the pupils at the club have taken the investigation further and begun to generalise. They have found a way to work out the number of "steps" in the longest possible route.
Laura S and Eleanor explain:
We found the longest route by taking the length (L), the amount of starting places there were (P) and then took (PxL) - (P-l) = The longest possible route.
Oliver, Laura S and Eleanor extended this to a path 4 paving stones wide:
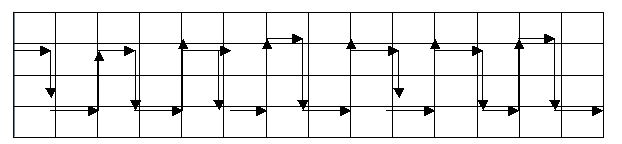
Laura S and Eleanor point out that "there are variations on this, which are just as long". Oliver says that he worked this out using
(PxL)-(P-2)
Perhaps you'd like to look into these patterns further.
