Trisected Triangle
Weekly Problem 34 - 2015
Four tiles are given. For which of them can three be placed together to form an equilateral triangle?
Four tiles are given. For which of them can three be placed together to form an equilateral triangle?
Problem
The diagram below shows four types of tile, each of which is made up of one or more equilateral triangles.
Image

For how many of these types of tile can we place three identical copies of the tile together, without gaps or overlaps, to make an equilateral triangle?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
If an equilateral triangle is split into a number of smaller identical equilateral triangles then there must be one small triangle on the top row, three small triangles on the row below, five small triangles in the row below that and so on.
So total number of small triangles is $1$ or $4$ or $9$ or $16$ etc. These are exactly the square numbers, the diagram below might help you to understand why.
Image
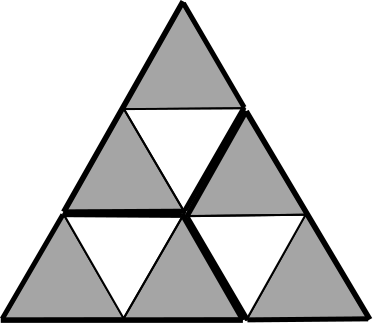
So, for three copies of a tile to form an equilateral triangle, the number of triangles which comprise the tile must be one third of a square number.
Of the four given tiles, only the third and fourth satisfy this condition, and both of these tiles can make equilateral triangles:
Image
Image