Forgot the numbers
On my calculator I divided one whole number by another whole number and got the answer 3.125. If the numbers are both under 50, what are they?
Problem
If you are a teacher click here for a version of the problem suitable for classroom use, together with supporting materials. Otherwise, read on ...

On my calculator I divided one whole number by another whole number and got the answer $3.125$.
I know that both numbers were less than $50$, but can't remember what they were.
Can you work out what they were?
Once you've had a chance to think about it, click below to see how four different pupils began working on the task.
Here is Gemma and Flo's work:
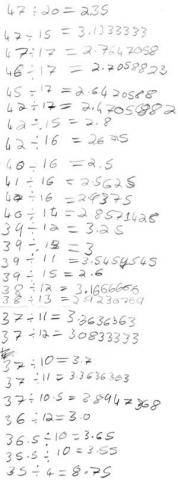
Details
For accessibility, the above work reads:
47 ÷ 20 = 2.35
47 ÷ 15 = 3.1333333
47 ÷ 17 = 2.7647058
46 ÷ 17 = 2.7058823
45 ÷ 17 = 2.6470568
42 ÷ 17 = 2.4705882
42 ÷ 15 = 2.8
42 ÷ 16 = 2.625
40 ÷ 16 = 2.5
41 ÷ 16 = 2.5675
42 ÷ 16 = 2.6375
40 ÷ 14 = 2.8571428
39 ÷ 12 = 3.25
39 ÷ 13 = 3
39 ÷ 11 = 3.5454545
39 ÷ 15 = 2.6
38 ÷ 12 = 3.1666666
38 ÷ 13 = 2.9230769
37 ÷ 11 = 3.3636363
37 ÷ 12 = 3.0833333
37 ÷ 10 = 3.7
37 ÷ 11 = 3.3636363
37 ÷ 10.5 = 3.8947368
36 ÷ 12 = 3.0
36.5 ÷ 10 = 3.65
35.5 ÷ 10 = 3.55
35 ÷ 4= 8.75
Richard wrote the following:
He explained:
"I multiplied $3.125$ by $1$, then I tried multiplying $3.125$ by $2$, then I multiplied $3.125$ by $3$ ..."
Here is the start of Thomas' work:
Can you take each of these starting ideas and develop it into a solution?
Getting Started
What do you know about division that might help?
Having a calculator to hand will be useful.
Have a look at each approach. What do you think he/she/they were doing?
How do you think that will help to solve the problem?
What do you think he/she/they would have done next?
Student Solutions
We had some good solutions submitted for this problem, here is a selection:
Het from Sudbury Primary School wrote the following:
The two numbers which the person divided by were 25 and 8. I worked this out by using Thomas's work, which said 0.125 is equivalent to 1/8 of 1. The first step I did was to multiply 8 by 0.125 so I got 1. Next I did 3 multiply by 8 to get 24. Next I added 24 and 1 to get 25. I did this because the question says that the sum was a whole divided by a whole so I had to get 3.125 into a whole number. Also we know that whatever the whole you have to divide 1 by 8 to 0.125.
The answer to this question is 25 divided by 8.
Matty from The British School in Manila, Philippines wrote:
The number is 3.125, its last digit is 5 (in the thousandths). Therefore, since the number is a whole number, and it ends in 5, we can keep multiplying by 2 to find the answer.
3.125 * 2 = 6.25
3.125 * 4 = 12.5
3.125 * 8 = 25
We have both numbers, 25 and 8! It cannot be simplified in any way, so our answer is 25 and 8!
A number of pupils from St. Mary's School contributed, namely, Cadence and Joanna; Kaya, Maisie and Arthur. Here is what they said:
We found out that 0.125 is equal to an eighth, and we knew that 8 multiplied by 3 equals 24,and 8 x 0.125 is 1, and 1 plus 24 is 25, so therefore 25 divided by eight is 3.125.
Thank you for this puzzle.
Tommy Farmer from St Georges Primary in Bickley wrote:
I knew as it ended in 0.125 that it had to be something divided by 8. So I calculated the inverse, ie, 3.125 x 8 and it gives an answer of 25.
So 25 divided by 8 (both numbers under 50) = 3.125.
Edward from Weston Favell Primary School wrote:
3.125 is equal to 3+1/8.
If we use algebra we can use M and C as the numbers we are looking for.
3 + 1/8 x M = C
I thought that we could times 3 by 8 and 1/8 by 8. It would equal 24 + 1= 25 so the numbers would be M = 8, C = 25
Ahan Singhal from Tanglin Trust School, Singapore sent in the following:
Since 0.125 is equal to 1/8, I need to multiply the number by 8 or a multiple of 8 to get a whole number. So, I start with multiplying 3.125 by 8, which gives me 25.
So, one option is 8 and 25.
If I double 25, it gives me 50 which is already outside the biggest number allowed (<50).
Therefore, the only possible answer is 25 and 8.
Tan Sze Qi from Innova Primary School in Singapore sent in the solution as an image.

Well done, these showed some good thinking as well as excellent explanations.
Teachers' Resources
Why do this problem?
Possible approach
Pose the problem orally, or project the text onto a screen, without mentioning the examples of how some children started. Give the class a few minutes to consider, individually, how they might go about tackling the problem, then pair them up and suggest that they talk to their partner about their ideas so far. Try to stand back and observe, and resist the temptation to make helpful suggestions!
Allow pairs to work on the task so that you feel they have made some progress, but do not worry if they have not completed it or if they report being stuck. The aim at this stage is for everyone to 'get into' the problem and work hard on trying to solve it, but not necessarily to achieve a final solution.
At a suitable time, hand out this (doc pdf) to pairs. Suggest to the class that when they've finished or can't make any further progress, they should look at the sheet showing three approaches used by children working on this task. Pose the question, "What might each do next? Can you take each of their starting ideas and develop them into a solution?". You may like pairs to record their work on large sheets of paper, which might be more easily shared with the rest of the class in the plenary.
Allow at least fifteen minutes for a final discussion. Invite some pairs to explain how the three different methods might be continued. You may find that some members of the class used completely different approaches when they worked on the task to begin with, so ask them to share their methods too. You can then facilitate a discussion about the advantages and disadvantages of each. Which way would they choose to use if they were presented with a similar task in the future? Why?
Key questions
How do you think this will help to solve the problem?
What do you think he/she/they would have done next?
Possible extension
Can they make up a similar question and solve it?
