One or Two
The diagrams show squares placed inside semicircles. What is the ratio of the shaded areas?
Problem
Image
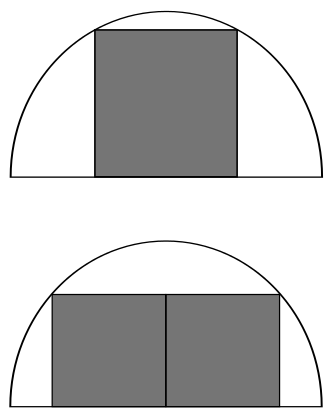
The diagrams show squares placed inside two identical semicircles. In the lower diagram the two squares are identical.
What is the ratio of the areas of the two shaded regions?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Image

Let the radius of each semicircle be $r$.
In the top diagram, let the side-length of the square be $2x$. By Pythagoras' Theorem,
$x^2 + (2x)^2 = r^2$ and so $5x^2 = r^2$. So this shaded area is $(2x)^2 = 4x^2 = \frac{4r^2}{5}$.
In the bottom diagram, let the side-length of each square be $y$. Then by Pythagoras' Theorem, $y^2 + y^2 = r^2$ and so $2y^2 = r^2$. So this shaded area is $r^2$.
Therefore the ratio of the two shaded areas is $\frac{4}{5} : 1 = 4 : 5$.
