Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Wipeout



- Problem
- Getting Started
- Submit a Solution
- Teachers' Resources
Why do this problem?
By working on this problem, students will develop their understanding of the mean, and will be prompted to reason, generalise and justify.
Possible approach
"Take the numbers 1, 2, 3, 4, 5, 6 and choose one to wipe out. Then find the mean of your remaining numbers."
Collect students' answers.
"Oh, that's interesting, two people (one person/no-one) got a whole number answer!"
"We're going to explore the possible answers for the mean when you wipe out one number, from the set of numbers from 1 to N, where N is even.
Is it always possible to wipe out a number and get a whole number answer for the mean?
Can it be done in more than one way?"
You may wish to give different groups of students different values of N to explore, or invite them to choose their own (even) values of N. Once they have explored, bring the class together to share findings.
There are several ways to prove that rubbing out 1 or N gives a whole number mean when N is even. Once either end is wiped out, we are left with an odd number of consecutive numbers, whose mean will be the middle number. This can be proved algebraically, or by considering an image such as the one below:
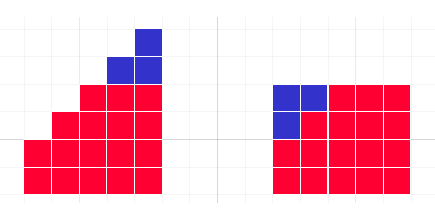
This picture, which can be generalised, shows that for a set of five consecutive numbers, the mean is equal to the median.
When you remove the largest value, N, the remaining mean is $\frac{N}{2}$.
When you remove the smallest value, 1, the remaining mean is $\frac{N}{2}+1$.
Since all the other possible means will lie between the two consecutive means $\frac{N}{2}$ and $\frac{N}{2}+1$, there can be no other whole number solutions.
Students can also explore the case where N is odd; in this case there is only one whole number solution, as all the means lie between $\frac{N}{2}$ and $\frac{N}{2}+1$.
Finally there are some puzzling questions (of increasing difficulty) that students can have a go at.
Key questions
For the "puzzling wipeouts":
If you know what the average is, and how many numbers you have, what can you say about the total?
If you know the average, what are the possibilities for how many numbers you started with?
If the average has a recurring decimal, how can this help you to work out what number you divided by?
Possible support
M, M and M and Unequal Averages are suitable problems for students to try in preparation for this problem.
Possible extension
Invite students to consider what the mean average could be when wiping out numbers from different sets such as:
- $71, 72, 73, 74, 75, 76$,
- $2, 4, 6, 8, 10$,
- $1000, 1004, 1008, 1012, 1016$

