Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangles in Circles
Age 11 to 14
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
Arielle and Ethan from Emanuel School in Australia considered drawing all of the possible triangles in the circle. Arielle said:
To solve this problem, I went to each dot and joined it with all of the other remaining dots, starting with the middle dot and then going clockwise around the circle. This means that you have connected all of the dots and that it is impossible to create anymore triangles.
As all of the triangles are on the same diagram, it is difficult to tell which is which and to count how many there are. Lexie from Walton High School in England used a systematic method to count the triangles. However, Lexie counts some of the triangles more than once - can you work out which ones?
You can make 36 triangles in the circle. This is because there are 9 triangles with 0 dots in between (three examples are shown below)
and 9 triangles with 1 dot inbetween. (two examples are shown below)
There are also 9 triangles with 2 dots inbetween and 9 with 3 dots inbetween. However there is no point in doing triangles with 4 dots inbetween because on the other side of the circle there is 3 dots so you would be counting those triangles for the second time. The same goes for 5,6 and 7 dots inbetween. Therefore, if there are 4 sets of 9, you can make 36 triangles in the circle.
Thanima from Eastlea Community School in the UK looked at the angles at the centre of the circle, as in the diagrams shown below:
When the band is changed form one peg to the next the difference in the angle at the centre will be 40 degrees:
360(the whole circle) $\div$ 9(number of pegs)
so the angle at the centre for each of the triangles will be 40, 80, 120 and 160 degrees.
Soham from Sutton Grammar School in England sent in a very full solution, going into detail about all of the different triangles. Soham began by labelling the pegs A to I, and then drawing on 7 triangles with side AB. Next, Soham considered triangles with side AC and so on. The angles are labelled. Soham has used Thanima's idea to find the angles - having found the angle at
the centre, the angles at the edges can then be found because the triangles are isosceles.
Click here to see Soham's work.
Lily from NLCS Jeju in South Korea noticed that she could do $180\div 9$ and then could find angles at the edge by doing $180\div9$ multiplied by how many 'segments' the opposite side used.
Click here to see Lily's work.
Why does Lily's method work?
Click here to see Soham's work.
Lily from NLCS Jeju in South Korea noticed that she could do $180\div 9$ and then could find angles at the edge by doing $180\div9$ multiplied by how many 'segments' the opposite side used.
Click here to see Lily's work.
Why does Lily's method work?
This diagram shows an angle opposite a 1-segment side in a red triangle, which Lily says is 20 degrees, and an angle at the centre in a green triangle, which Thanima showed is 40 degrees.
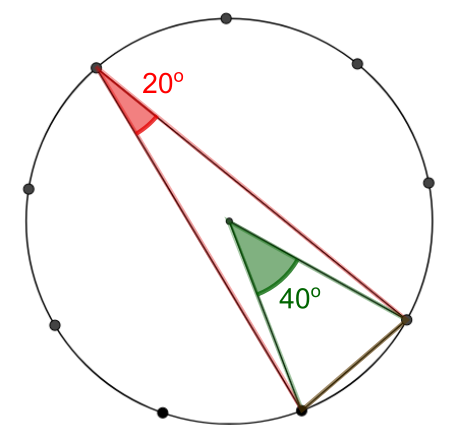
These two triangles share a base, and one of them has the other angle at the centre while the other has its other angle on the circumference. There is a special relationship between these two angles!
Can you discover the relationship by finding these angles for other examples?
Can you discover, or explain, the relationship using a diagram like the one below?
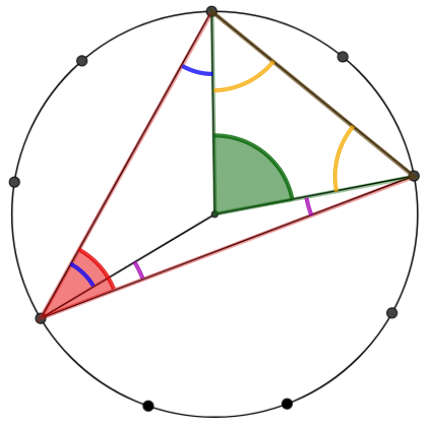
And what about if the red triangle doesn't contain the centre?

