Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tilted Squares



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to everyone who submitted a solution to this problem - we received a very large number!
Can you find a quick and easy method to work out the areas of tilted squares?
Phoebe from Long Field Spencer Academy, Harry B from St Johns College School and Meher, all in the UK, used counting methods. Phoebe and Harry counted the squares in the underlying grid. Harry B's work is shown below. Harry has labelled with '1' the pieces which add up to the 'first' square counted, then with '2' the pieces which add up to the 'second' square counted, and so on.
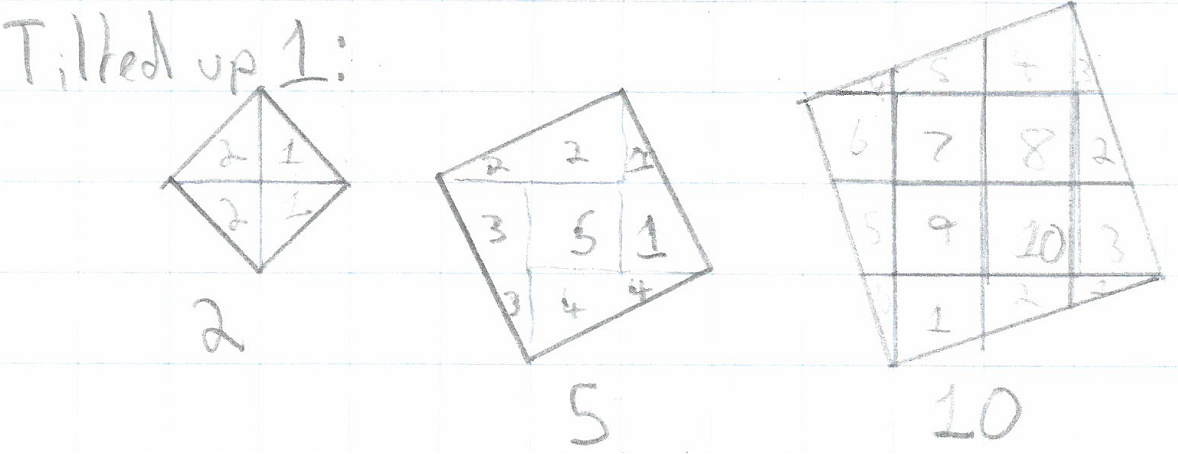
Meher counted dots using the method shown below. Why does Meher's method work?
To get the area of a tilted square, you have to count how many dots there are inside a square. This will clearly tell you the area.
Leonardo from The British School of Milan and Cole suggested rotating the tilted square to find its area. Leonardo wrote:
A quick method to find their area is just to bring the tilt the square back to normal and the area will be the same as the tilted one.
A way to prove them is easy. Draw a 2 by 2 square. Tilt it once. As you can see the square is still 2 by 2, so the area will still be 4.
The answer will still be a square number.
But for the tilted squares shown in the problem, the side length of the tilted square might not be a whole number...
Sophia from Kings Way School in New Zealand, Elaine and Jenna from New Zealand, Grace and Isla from Long Field Spencer Academy, Adam from Heckmondwike Grammar School in the UK, Holly-Hope and Annabelle from Jersey School for Girls in Jersey, Rafsan from Dulwich College in the UK, Adam M, Adam B, Anika and Lucia from King's School Dubai, Tejas, Ruhi, Valerie, Mithravinda, Rivaan, Kabir, Akshobhyan, Nithya, Deethya, Uday, Udit, Tarikha, Kashvi, Swathi, Devasena, Arnav, Samarth and Shubhangee from Ganit Kreeda in India, Riley and Mar all used a method that involved drawing a larger square and working out the areas of triangles. This is Annabelle's work:

Dan and Freya from Long Field Spencer Academy used a similar method that involved using a smaller square inside the tilted square, and four triangles. This is Dan's work:

Adam and Jack from Heckmondwike Grammar School, Lamech from Dulwich College in the UK and Monty J used Pythagoras' Theorem to find the areas of the tilted squares. This is Lamech's work:

Notice anything special about their areas?
Can you predict the areas of other squares with a tilt of 1?
Using the method of drawing a larger, horizontal/vertical square and subtracting the four triangles, Rafsan noticed something about the areas of the triangles:
0.5 is really and truly the star number here as when moving [between two] tilted squares, we add 0.5 [to the area of each little triangle].
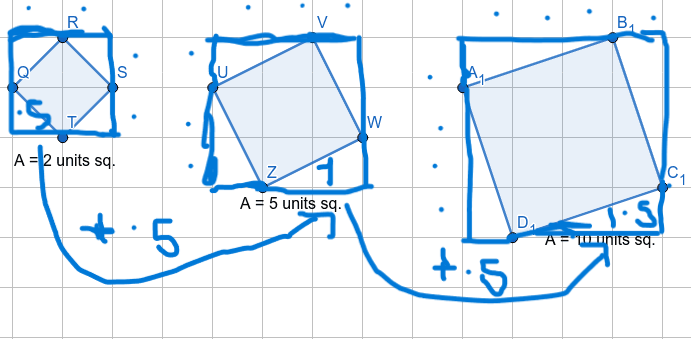
Freya noticed a pattern in the areas of the squares - and used Rafsan's idea:
I looked at the pattern of the previous areas of the squares within the squares. They were all square numbers in order, so I based my prediction on this. I figured out how to find the area of the triangles by looking back at what I did earlier. This followed a pattern of increasing by half a square cm per triangle.
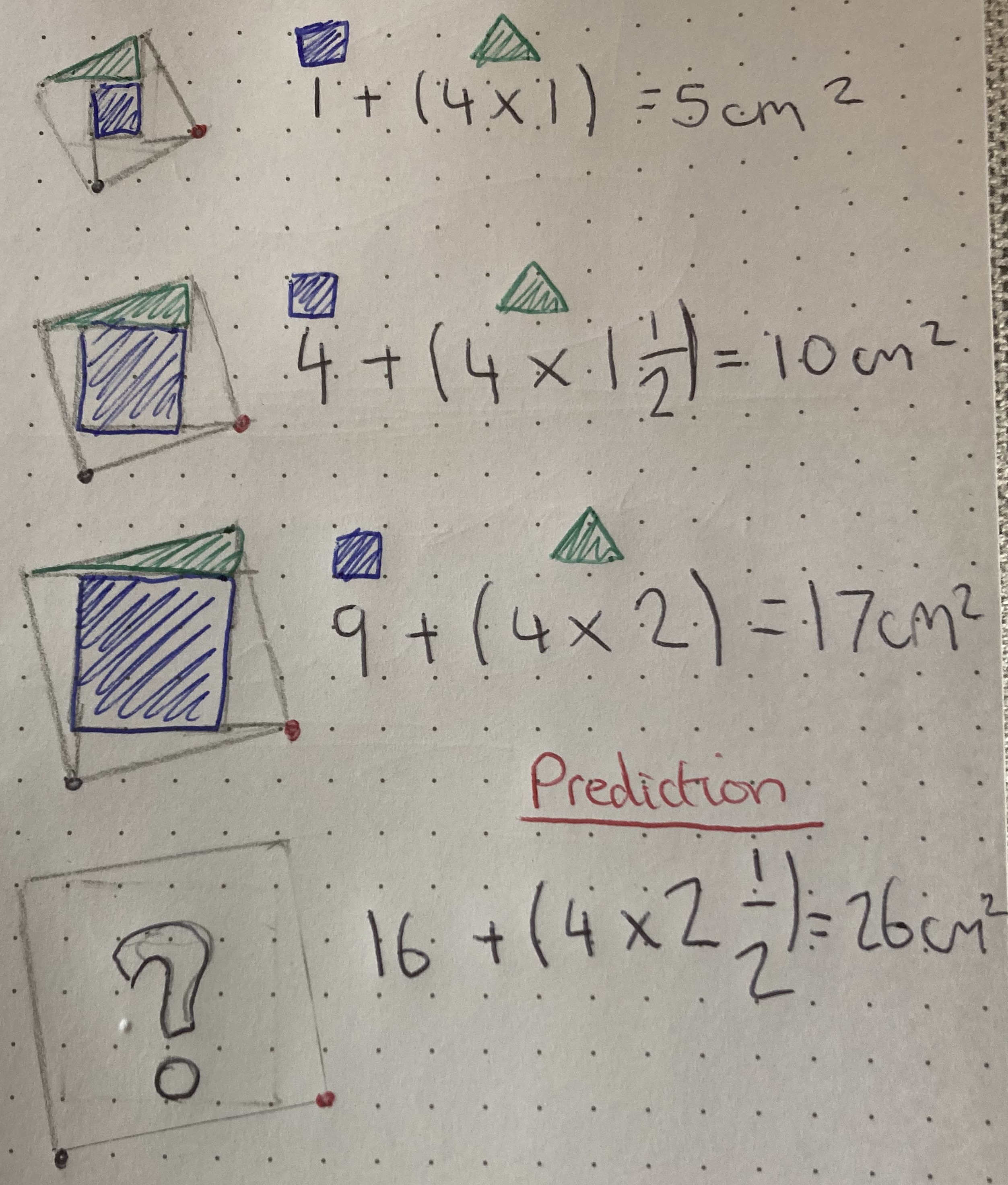
Harry B and the students from Ganit Kreeda recorded their results in a table to help spot patterns. This is Ganit Kreeda's work:
Harry B noticed the same thing that Ganit Kreeda have in the "Observation" column:
along$^2$ + 1 = area
$a^2+a =$area
Conclusion: The area of a square that has been tilted up one is the horizontal base squared add 1.
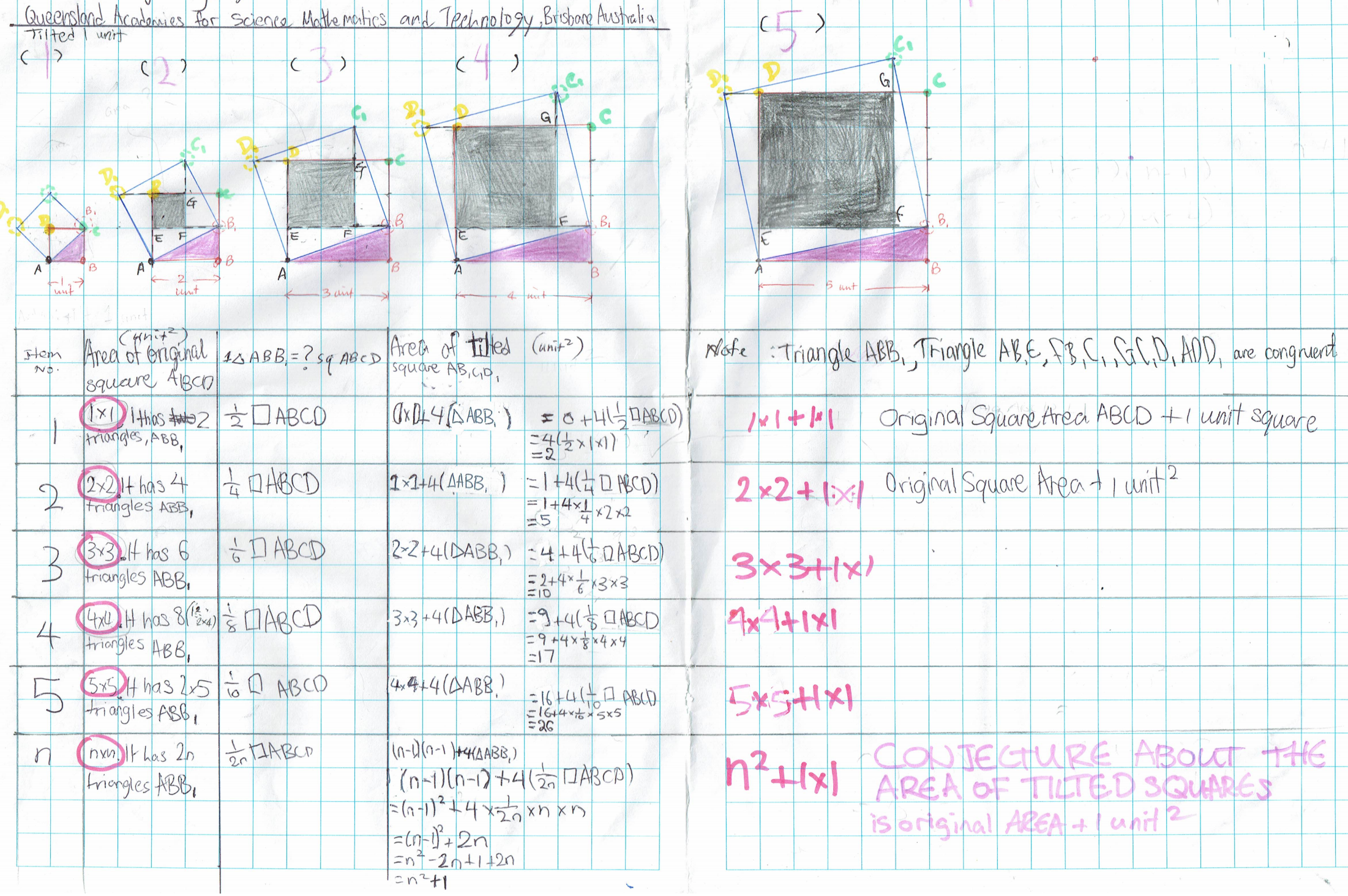
Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia noticed the same pattern. Ci Hui also made a table to show the areas of the squares. Ci Hui's method for finding the areas is also different to the methods shown above (although similar to Dan and Freya's method), and is explained in the table. Click to see Ci Hui's table and method.
What about squares with a tilt of 2? Or 3? Or 4? Or...?
The students from Ganit Kreeda, Harry B and Ci Hui also made tables to record the areas of squares with other tilts. This is Ganit Kreeda's work:
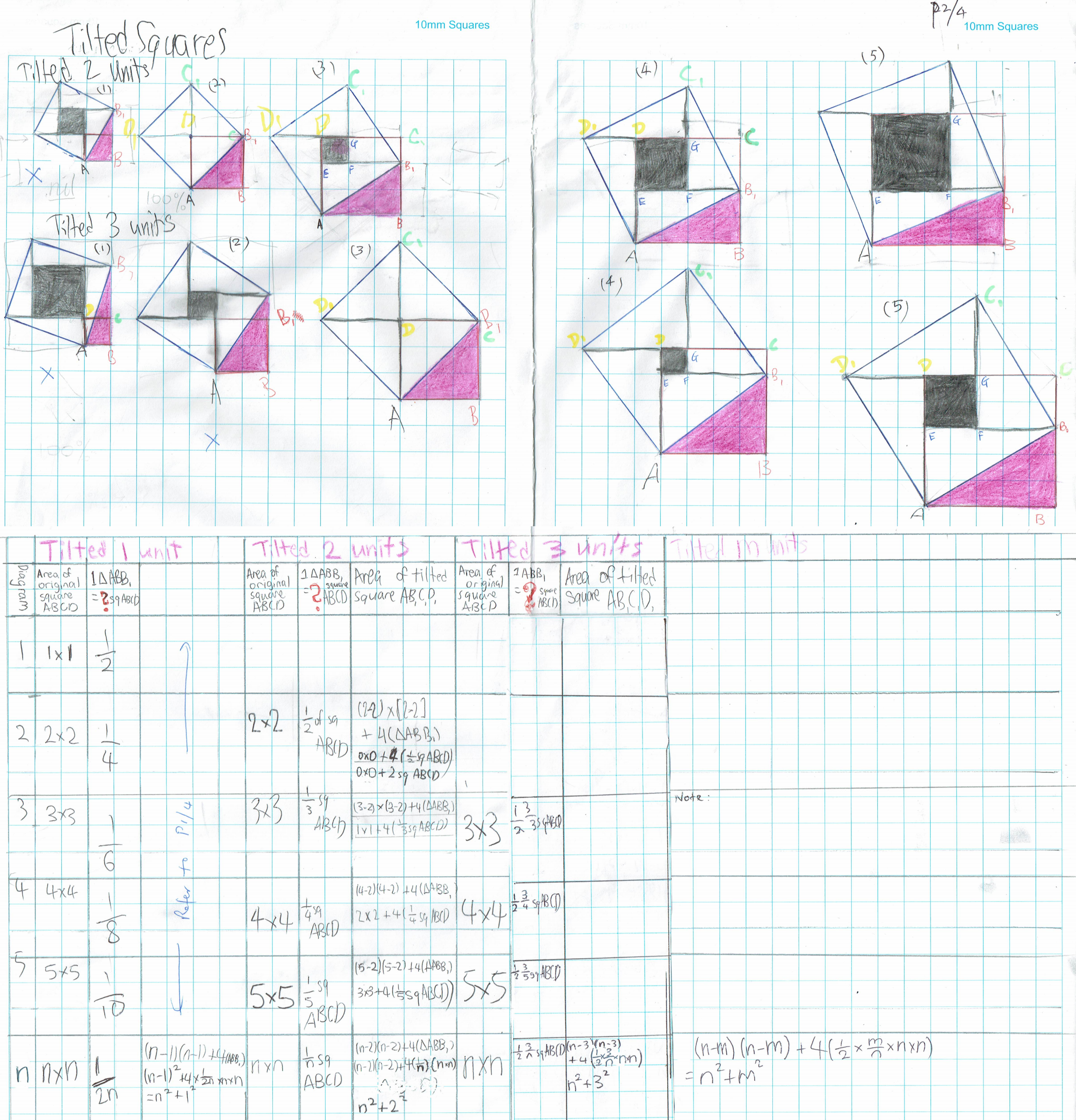
Harry B, Ci Hui and Shaunak from Ganit Manthan described the same pattern. Harry B began from the original counting squares method, and Ci Hui used the same method as before. Click to see Ci Hui's method applied to squares of tilt 2 and 3, and Ci Hui's table.
Can you make any conjectures about the areas of tilted squares?
Can you prove your conjectures?
Harry B had noticed that The area of a square that has been tilted up one is the horizontal base squared add 1. Harry B used the method described by Dan and Freya to prove this. Here is Harry B's proof:
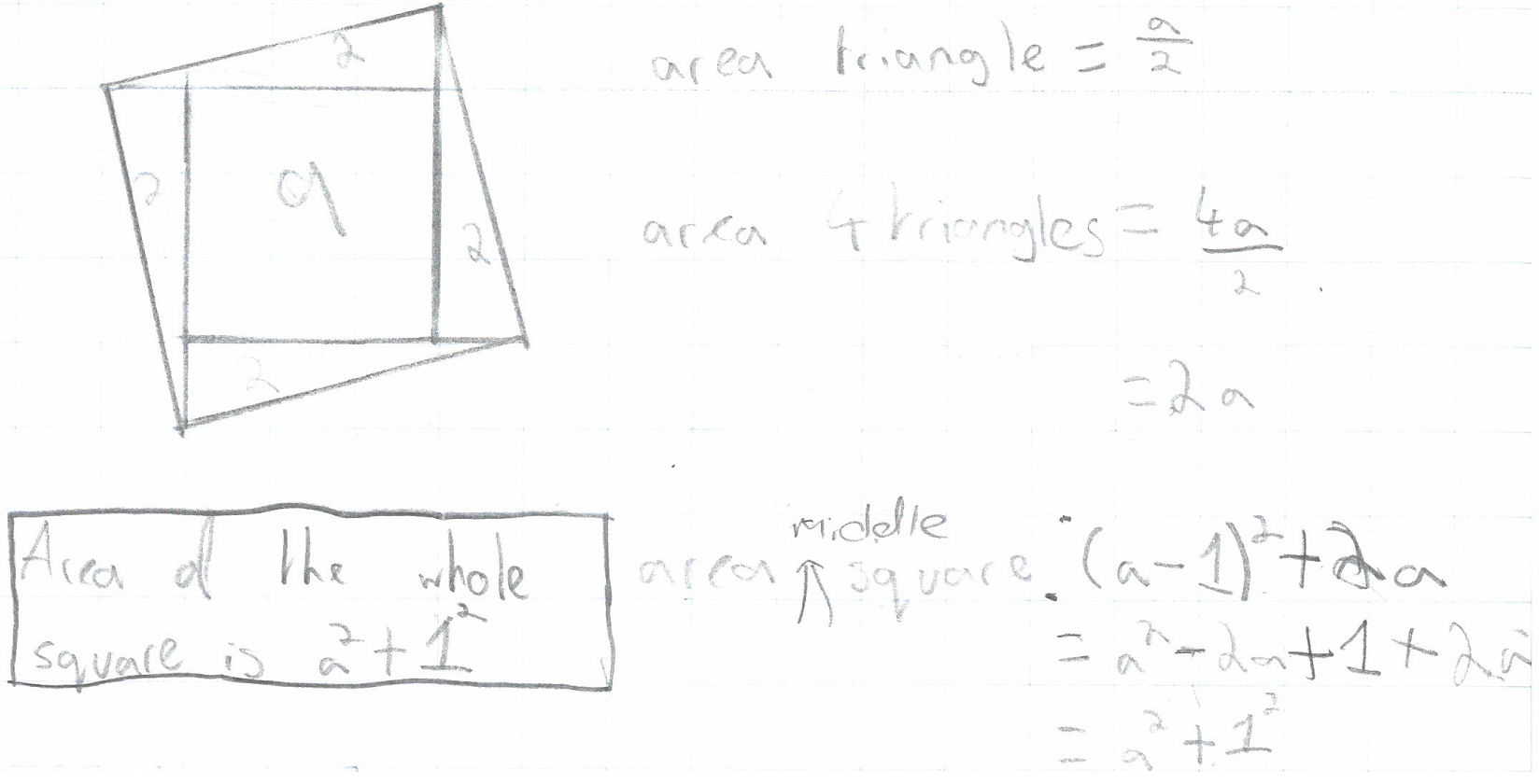
The students from Ganit Kreeda had noticed that Tilt area = square area + (tilt)$^2$. They used another method involving four triangles to prove their conjecture:
From fig 1:
Area of tilted square = Area of white part
We then cut blue 4 triangles and rearrange them to form 2 rectanges as shown in fig 2:
So, area of the tilted square = area of the white part = $n^2 + t^2$
They also noticed some other things:
Area of the outer square (with side $n+t$) $= (n+t)^2$
It is clear from fig 2:
Area of outer square $= n^2 + t^2 + 2nt$
Therefore $(n+t)^2 = n^2 + t^2 + 2nt$
We proved and explained pictorially the identity $(a+b)^2=a^2+b^2+2ab$
Also, we proved Pythagoras theorem, since
Area of tilted square $= n^2+t^2$
Side of tilted square $\sqrt{n^2+t^2}$.
Adam M, Adam B, Anika and Lucia derived a formula for the area of a tilted square using the method of subtracting the areas of four triangles from the area of the larger square. This is their work, with two diagrams and a small correction added:

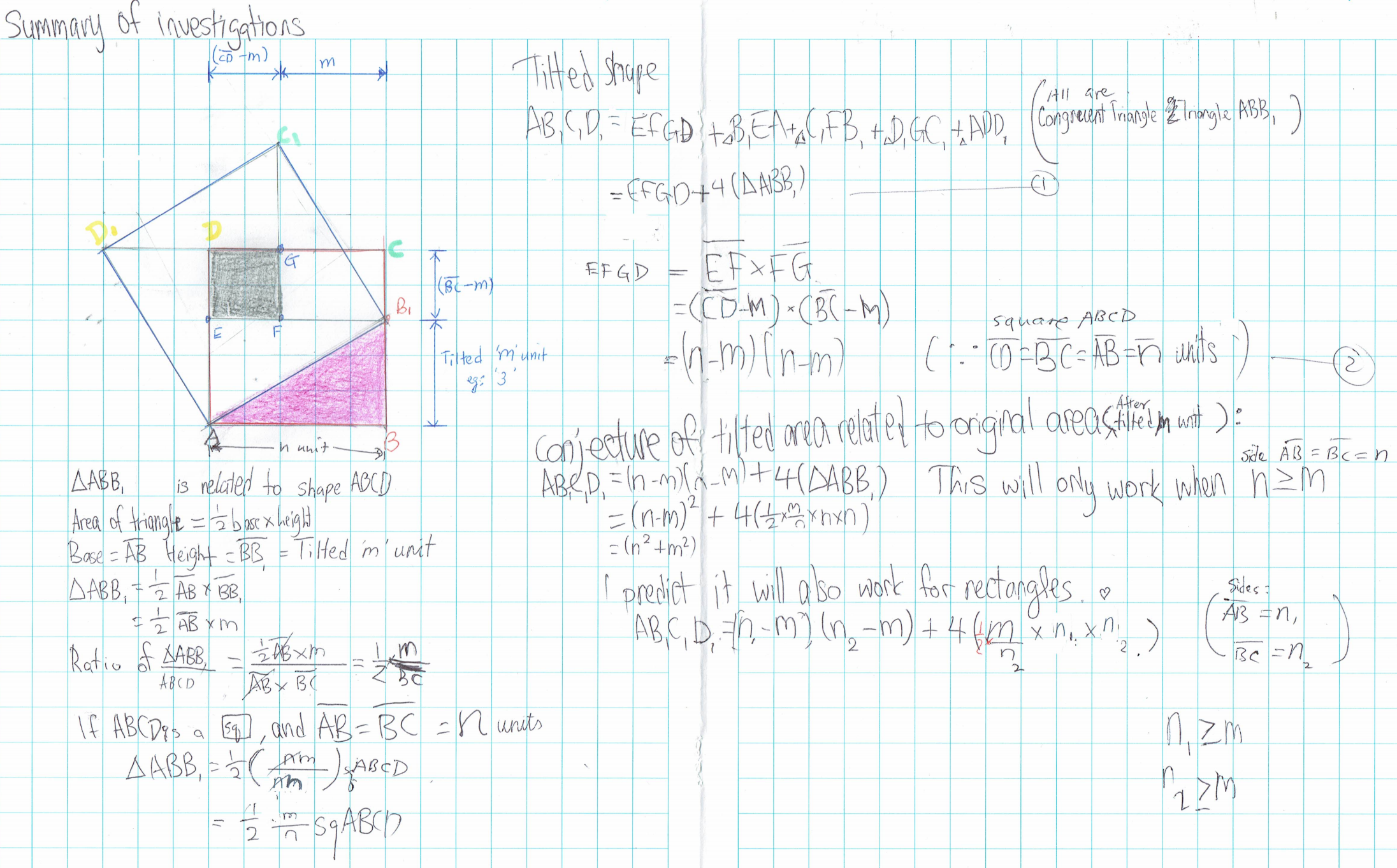
Notice that they use different letters for the base and height of the larger square. If they used $h$ for both, then the final formula would be $h^2 - 2th + 2t^2$, which can be factorised to $(h-t)^2 + t^2.$ Can you see how this is related to the formulas proved by Harry B and the students from Ganit Kreeda?
The students from Ganit Kreeda and Harry B came across Pythagoras' Theorem when they explored and proved their conjectures. Some people worked the other way round - they used Pythagoras' Theorem to prove the formula. Umar from Eastcourt Independent School in the UK, Wenxuan from St George's International British School in Italy, Tamin from Canada, Muhammad, Adam from Heckmondwike Grammar School and Lamech used Pythagoras' Theorem to find the area of a tilted square. This is Tamin's work:
This is Adam's work:
By using the Pythagorean theorem ($a^2 + b^2 = c^2$) you can calculate one side of the square which you can then use to find the area.
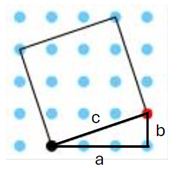
This calculation can be further simplified into one equation.
Area $=\sqrt{a^2+b^2}\times\sqrt{a^2+b^2}=a^2+b^2$
This can be shown through a well-known diagram explaining the Pythagorean theorem.
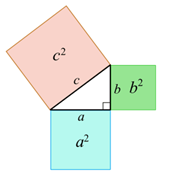
Ci Hui used the same method as before to prove the formula for the area of a tilted square. Ci Hui also made a conjecture about the areas of tilted rectangles. Click to see Ci Hui's work.