Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tet-trouble



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The following solution was sent in by Becki from the Mount School, York. Becki uses The Triangle Inequality. Andy from the Garden International School used the same method .
It is definitely impossible to have a tetrahedron which has edge lengths of 10, 20, 30, 40, 50 and 60 units.
This is because to produce a triangle two sides have to be bigger (when added together) than the third. So this tetrahedron won't work because the 10 is too small to make a triangle. e.g. 10, 20, 30
- 20 + 30 > 10 (OK)
- 10 + 30 > 20 (OK)
- but 10 + 20 = 30 so the triangle becomes a straight line.
10 will not go with any other two numbers in the above list.
However it is possible to make a tetrahedron which has lengths 10, 20, 25, 45, 50 and 60 units. The reason is that the numbers are big and small enough to fit the rule of triangles (the sum of two sides bigger than the third) Here is my net of this tetrahedron to explain my answer (not to scale!)
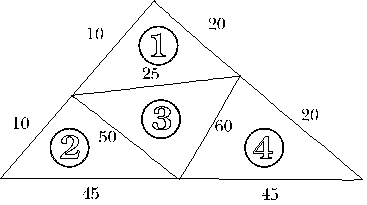
| Triangle 1 | 10 + 25 > 20 | Triangle 2 | 10 + 50 > 45 | |
| 10 + 20 > 25 | 10 + 45 > 50 | |||
| 20 + 25 > 10 | 50 + 45 > 10 | |||
| Triangle 3 | 50 + 60 > 25 | Triangle 4 | 60 + 45 > 20 | |
| 25 + 60 > 50 | 20 + 60 > 45 | |||
| 25 + 50 > 60 | 20 + 45 > 60 |
So all four faces are fine, so it can make a tetrahedron.

