Related Collections

You may also like

I'm Eight

Find a great variety of ways of asking questions which make 8.

Let's Investigate Triangles

Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?

Noah

Noah saw 12 legs walk by into the Ark. How many creatures did he see?

Strike it Out

Age 5 to 11
Challenge Level

Strike it Out

Watch the video below which shows two people playing the first few turns of a game.

What do you notice?
What do you want to ask?



If you can't access YouTube, here is a direct link to the video.

Watch the video a second time.

Can you work out how to play the game?  
What do you think the rules might be? 
How might someone win the game?

If you are unable to view the video, you could click through this powerpoint presentation, which also demonstrates how to play. Alternatively, the rules of the game are hidden below.

The aim of the game:
The player who stops their opponent from being able to go wins the game.
 

How to play:
  • Start by drawing a number line from 0 to 20 like this:


0-20 number line

(You can find some of these number lines here.) 

  • The first player chooses a number on the line and crosses it out. The same player then chooses a second number and crosses that out too. Finally, he or she circles the sum or difference of the two numbers and writes down the calculation.

For example, the first player's go could look like this:

first player's go: 3+8=11

  • The second player must start by crossing off the number that player 1 has just circled. He or she then chooses another number to cross out and then circles a third number which is the sum or difference of the two crossed-off numbers. Player 2 also writes down their calculation.

For example, once the second player has had a turn, the game could look like this:

player 2: 11+9=20

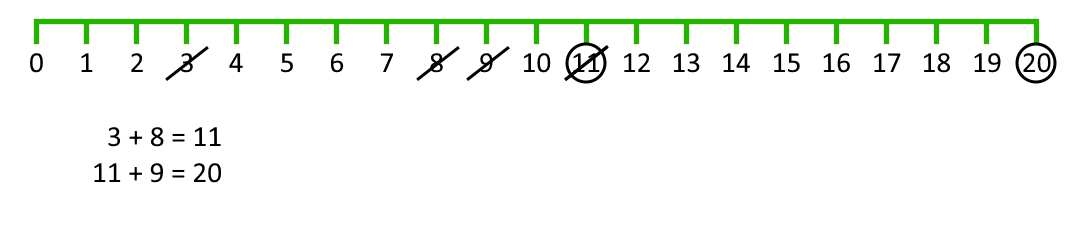
  • Play continues in this way with each player starting with the number that has just been circled.
  • Once a number has been used in a calculation, it cannot be used again.
  • The game ends when one player cannot make a calculation. The other player is the winner.

It's your turn!
Try playing the game against someone else a few times to get a feel for it.
Do you have any good ways of winning?

 

Now it's time to work together with a partner, rather than against them.
Try to create a string of calculations that uses as many numbers as possible on the 0-20 number line.
Is it possible to create a string of number sentences that uses all the numbers on the 0-20 number line? Why or why not? How would you convince a mathematician?

Once you've had a good think about it, you may like to look at this proof that has been scrambled up.
Can you rearrange it into its original order?

If you would prefer to work away from a screen, you could print off, cut up and rearrange the statements on this sheet (it includes three copies of each statement).

 

What about the 1-20 number line? Is it possible to create a string of number sentences that uses all the numbers on the 1-20 number line? Why or why not? How would you convince a mathematician?

Again, once you have thought about it, you may like to look at this proof that has been scrambled up.
Can you rearrange it into its original order?

If you would prefer to work away from a screen, you could print off, cut up and rearrange the statements on this sheet (it includes two copies of each statement).

Click here for a poster of this problem.

Why play this game?

This game offers an engaging context for practising addition and subtraction, but it also requires some strategic thinking. The collaborative version provides a fantastic opportunity for learners to reason mathematically, and to experience proof.
 
The game also offers the chance to focus on any of the five key ingredients that characterise successful mathematicians. The collaborative version lends itself particularly to fostering a positive attitude to mathematics as learners' resilience may be tested!

 

Possible approach

This problem featured in an NRICH Primary webinar in October 2020.
 
Show the video to the group, explaining that there is no sound as such and inviting them to think about what they notice and what they want to ask. (You could click through this powerpoint presentation one 'go' at a time if you cannot access the video.) Having watched it once, give them an opportunity to talk to a partner and then collect some of their questions and 'noticings' on the board. Encourage other members of the class to respond rather than you. Before playing the video a second time, explain that as they're watching, you'd like them to consider what the rules of the game might be. Mediate a discussion following the second viewing so that the class comes to an agreement about the rules of the game and how a player wins.
 
Give children time to play several games in pairs so they get a feel for it. A set of printable number lines can be found here. Share some of their strategies and then ask them whether they think it might be possible to cross off all the numbers in a game. Give them time to work co-operatively with their partner on this challenge before bringing them together again to see what they have found out. You could find out whether, for example, any pairs have used more than half the numbers. More than fifteen numbers? Given enough time, do they think they could find a way to use all the numbers? Some will have realised that it is impossible to cross off zero - encourage them to explain why this is the case. To give them an example of the kind of reasoning that constitutes a proof, you could share this proof sorter with them. It includes all the steps to create a watertight chain of reasoning, but muddled up. The challenge is to put the statements in the correct order. (If you would prefer learners to be working away from a screen, you could print off and cut up copies of this sheet, which contains three copies of the statements.)
 
Learners could then investigate whether it is possible to use all the numbers if the number line goes from 1 to 20 instead. Give them chance to explore this new scenario in pairs. Many will be able to reason that it is still not possible due to there being an even number of numbers in total. Again, you could work on this proof sorter as a class, ordering the statements to help learners get to grips with the idea of proof. (Alternatively, you could print off this sheet, which contains two copies of the proof sorter statements.)
 
 

Key questions

Have you found any good ways to beat your opponent?
Can you cross out all the numbers in one game? How do you know?
What is the biggest number of numbers you can cross out?
 

Possible support

If children are struggling with the calculations, a shorter number line may be appropriate so focusing on a number line to 10 still elicits many of the same ideas about possibilities and outcomes as well as the way in which the operations of addition and subtraction work on a limited set of numbers.
 

Possible extension

Can children reason whether it would be possible to use all the numbers on any number line of consecutive numbers? (They may like to unscramble this proof sorter, or use a printed copy of the statements.)
Children can suggest their own 'what if ...?' questions, for example:
What if we could use multiplication/division?
What if we drew a longer number line?
What would happen if we included decimal numbers in our number line?
What if the number line extended beyond zero to negative numbers?

The possibilities are endless but do make sure they try out their new version of the game to check it is a 'good' game.


The Highland Numeracy Team in Scotland kindly shared this pdf with us, which contains ideas for adaptating Strike It Out. Some variations include the use of concrete materials suited to the version of the game, such as tens frames, Dienes, or place value counters.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.