Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Square Coordinates
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Hannah tackled the first part of this problem. Here are the squares she drew:
(a)
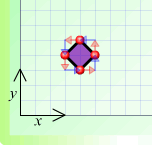 (b)
(b)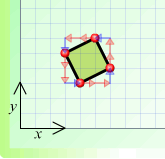 (c)
(c)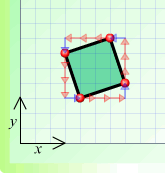
(d)
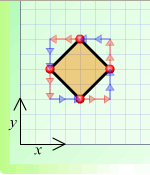 (e)
(e)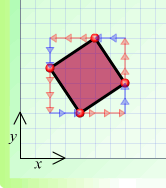
In all of these, the side AB could either be from the bottom corner to the right, or from the left corner to the top. Do you see why?
Hannah went on to complete the arrow notation for these squares. She's taken the side AB to be from the bottom up to the right.
(a) $A 1 \rightarrow +1 \uparrow B 1 \leftarrow + 1 \uparrow C 1 \leftarrow + 1 \downarrow D 1 \rightarrow + 1 \downarrow A$
(b) $A 2 \rightarrow + 1 \uparrow B 1 \leftarrow + 2 \uparrow C 2 \leftarrow + 1 \downarrow D 1 \rightarrow + 2 \downarrow A$
(c) $A 3 \rightarrow + 1 \uparrow B 1 \leftarrow + 3 \uparrow C 3 \leftarrow + 1 \downarrow D 1 \rightarrow + 3 \downarrow A$
(d) $A 2 \rightarrow + 2 \uparrow B 2 \leftarrow + 2 \uparrow C 2 \leftarrow + 2 \downarrow D 2 \rightarrow + 2 \downarrow A$
(e) $A 3 \rightarrow + 2 \uparrow B 2 \leftarrow + 3 \uparrow C 3 \leftarrow + 2 \downarrow D 2 \rightarrow + 3 \downarrow A$
Good work, Hannah!
Ahmed gave us instructions to construct a
square where you are given one of its sides:
Suppose you're given the side $A a \rightarrow + b \uparrow B$. (I noticed that $\downarrow$ could be written as $-\uparrow$ and $\leftarrow$ could be written as $-\rightarrow$, so $a$ and $b$ could be negative, but that doesn't matter. This makes it a bit easier, as we only have two sorts of arrow then.) Then the square is either $$A a \rightarrow + b \uparrow B -b \rightarrow +a \uparrow C -a \rightarrow -b \uparrow D b \rightarrow -a \uparrow A$$ or $$A a \rightarrow + b \uparrow B b \rightarrow -a \uparrow C -a \rightarrow - b \uparrow D -b \rightarrow + a \uparrow A.$$
Well done, Ahmed, especially for spotting
that there are two possible squares.
Ahmed then worked out which of the collections of points could
be a square.
- (8,3), (7,8), (2,7), (3,2). In arrow notation, this would be $A -1 \rightarrow +5 \uparrow B -5 \rightarrow - 1 \uparrow C 1 \rightarrow - 5 \uparrow D 5 \rightarrow + 1 \uparrow A$. This is of the first form, with $a=-1$ and $b=5$. So this is a square.
- (3,3), (7,4), (8,8), (4,7). In arrow notation, this would be $A 4 \rightarrow + 1 \uparrow B 1 \rightarrow + 4 \uparrow C -4 \rightarrow - 1 \uparrow D -1 \rightarrow - 4 \uparrow D$. This isn't of either form, so the points don't form a square.
- (16,19), (18,22), (21,20), (19,17). In arrow notation, this would be $A 2 \rightarrow + 3 \uparrow B 3 \rightarrow - 2 \uparrow C -2 \rightarrow - 3 \uparrow D -3 \rightarrow + 2 \uparrow A$. This is of the second form, with $a=2$ and $b=3$, so the points form a square.
- (4,20), (21,19), (20,2), (3,3). In arrow notation, this would be $A 17 \rightarrow - 1 \uparrow B -1 \rightarrow - 17 \uparrow C -17 \rightarrow + 1\uparrow D 1 \rightarrow + 17\uparrow A$. This is also of the second form, with $a=17$ and $b=-1$, so the points form a square.

