Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Sets of Numbers
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Sets of Numbers
How many different sets of numbers with at least four members can you find in the numbers in this box?
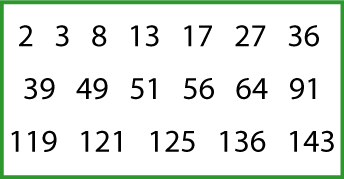
For example, one set could be multiples of $4$ {$8, 36 ...$}, another could be odd numbers {$3, 13 ...$}.
Why do this problem?
This problem gives plenty of opportunity for both discussion and exploring patterns, properties and relationships involving numbers. It also helps learners to make general statements about properties of numbers such as squares, factors, multiples, odd and even, and to identify examples for which a statement is true or false.Possible approach
You could also use this interactivity as a starter to this problem where you drag numbers you "like" (i.e. are part of a set) to one side and numbers you "don't like" (i.e. are not in your set) to the other. The children then have to ask questions with yes/no answers to determine the name of your set. You could invite some learners to take the
lead on this themselves, with the rest of the group asking questions.
You could then introduce the problem itself and learners could work in pairs from this sheet so that they are able to talk through their ideas with a partner. (The sheet has two copies of the box of numbers on it.) You could also challenge pairs to find two other
possible members for their sets from the numbers under $150$.
At the end learners could be asked for the titles of the sets they have found and then others could suggest members for these sets. You could make statements such as "$9$ is a member of this set" and ask learners to identify whether the statement is true or false. When sets of multiples of $2$, $4$ and $8$ have been found and discussed, learners could be asked to explain why no other sets of
multiples of even numbers are possible from the numbers in the box.
Key questions
What can you tell me about this number?
Is this odd or even? What else do you know about it?
Which multiplication tables will you find this number in?
Can you see any other multiples of that number?
Can you suggest other numbers that could go together in this set?

