Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Nine Colours
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Shriya from International School Frankfurt in Germany, Ahmed from Norlington School in the UK, Luis from King's College Alicante in Spain, Kenneth from Network International School in Myanmar, Savannah, Hugo, Mieke, Kristina, Benji, Dayeon, Jenny, Maddy and Dominika from British International School of Bratislava in Slovakia, Rudy from Priory School in the UK and David from Colegio Decroly Americano in Guatemala, who all sent in correct cubes.
Ikroop and Wan from Maple Leaf Foreign Nationals School in China sent in a simple and very neat way of making the cube:
First we put 3 colours in a group because we thought it would be easier.
Next we made rods of 3 blocks. Each rod had 1 of its group's colours. We had to make sure the colours in each rod were in a different order.
Afterwards we took one rod of each colour group and connected them to make a square. We did this with the remaining rods, making three squares. We did not flip or rotate the rods, but connected them strategically, making sure that the rods of each colour group were ordered differently in each square.
Lastly we stacked all the squares, one on top of the other. When we finished, our cube had 1 of every colour in each face!

Oengus from West Island School in Hong Kong coloured the cube layer by layer:Lastly we stacked all the squares, one on top of the other. When we finished, our cube had 1 of every colour in each face!
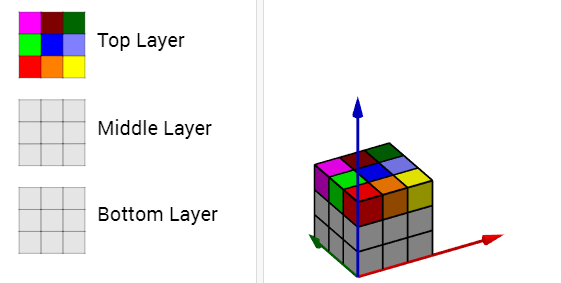
Firstly, we fill the whole top layer with random colours of your choice, but not using the same colour twice. Like this!
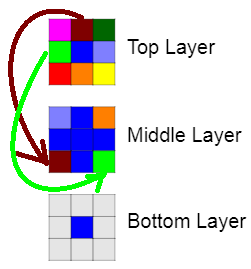 Next, you figure out which colour you put in the middle of the top layer - in this case blue - and put them in the middle of every face, this makes sure that your blue cannot be a cause in a mistake as it is definitely not on the same face as another. Now the
colour blue is eliminated as it is on every face, this way, you don't have to worry about it anymore.
Next, you figure out which colour you put in the middle of the top layer - in this case blue - and put them in the middle of every face, this makes sure that your blue cannot be a cause in a mistake as it is definitely not on the same face as another. Now the
colour blue is eliminated as it is on every face, this way, you don't have to worry about it anymore.After we have eliminated a colour, the middle layer only needs 4 cubes to finish it. The corners of the layer. We have just looked at the pieces with next to the blue piece on top. We duplicate them on the layer below but put them on the other side of the layer and move them left once.
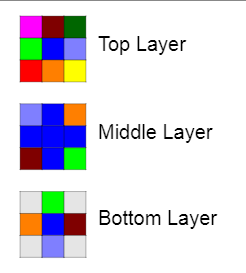
For the bottom layer, first I have used the same colours as the last step and done exactly the same actions as last step. But there is one difference: instead of moving the colour left once, I move it right, which again makes sure that we do not have the same colour on one face.
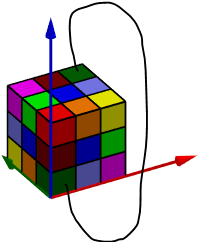
The final step, the simplest of them all, all we have to do is get the corners from the top layer, and put them opposite on the bottom layer, like shown in the image to the right.
Jorge from Dronfield Henry Franshawe in the UK started with the corners:
I first started out the problem by colouring the corner cubes in as they have the largest surface area and take up 3 squares. I did thus so that only two cubes of 1 colour filled all 6 sides if you place them on opposite sides of the 3$\times$3$\times$3. I then did this with 4 colours so there was only 5 squares left on each side, which allowed me to then fill in the cubes which
Rishika from Nonsuch High School for Girls in the UK, Anny from St Mary's School Cambridge, Kevin from Harrow International School Hong Kong and Andrew from Davenies School in the UK also thought about corner cubes, edge cubes and middle cubes to find a solution. This is Anny's work:
A corner cube is shown on 3 faces, an edge cube is shown on 2 faces, a middle cube is shown on 1 face and the centre cube is not shown at all.
The 1 colour cube that has 1 in the centre has to make the best use of the remaining 2 cubes, which has to be 2 opposite corners.
Then the remaining 6 corners would each have a set of cubes of a certain colour. The set would contain 1 corner cube, 1 edge cube and 1 middle cube.
(Green opposite pink, orange opposite yellow, dark blue opposite light blue.)
I put the greens first and had each pink opposite the matching green on the big cube.
I did the same with the rest.
Orange and yellow Dark and light blue
Finally, I placed the browns and dark greens which were on the edges.
Notice that in some way, Oengus' solution is different to the others, because all of Oengus' faces have the same colour cube in the middle, but all of Anny's faces and all of Ikroop and Wan's faces have different colours in the middle. What about Jorge's solution? Do Anny's solution and Ikroop and Wan's solution follow the same pattern, or is there a difference between those too? How many truly different solutions are possible?
Andrew's solution provides the basis of an idea on this:
I worked on the principle that you could have 3, 2 or 1 on show (on a corner cube, edge cube and middle cube respectively), and each colour has to add up to 6 (because there are 6 faces). I also used 6 different coloured cubes in the middle as my starting point

