Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
More Number Pyramids
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Ashley from Chase Terrace Technology College in the UK noticed some patterns between the numbers:
the bottom row is always the bottom left hand corner plus 1 like so 4,5,_,_. Then to find the second from the right on the bottom you would do the second from the left add 1 like so 4,5,6,_. To figure out the last number on the bottom you just add on 1 one to the second from the left and you would get the answer of 4,5,6,7. From there you can figure out the top one using the number pyramid.
Maxim from Hart Plain Junior School in the UK, Leslie from Westrige School in the USA and Julia and Na Yoon from Dulwich College Seoul in South Korea found ways to find the last number from the first number using patterns. This is Maxim's method:
$8n+12$
I worked this out by entering consecutive numbers beginning from $0$ and trying to spot a pattern. I realised that every number had a difference of $8$ and all numbers were $12$ off a multiple of $8$.
This is Leslie's method:
You can work out the top number if given the number in the bottom left hand corner. You know that the numbers are consecutive on the bottom layer, so you take the sum of the four numbers on the bottom layer of the pyramid and multiply it by two. For example, if the bottom number is 0, you do 0+1+2+3, the numbers in the bottom layer. Then, you multiply this result by 2, and you get the correct answer, 12. This method works with decimals and if the pyramid goes by twos or threes.
Rik from G.D.Goenka World School in India, Anh Minh from British Vietnamese International School Hanoi in Vietnam and Julia and Na Yoon used algebra to find the top number. This is Julia and Na Yoon's work:
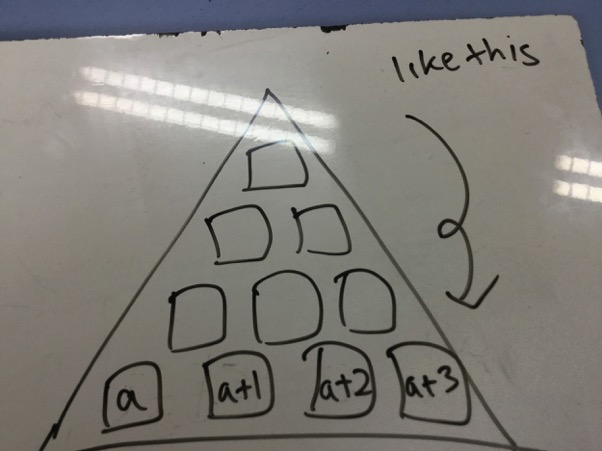
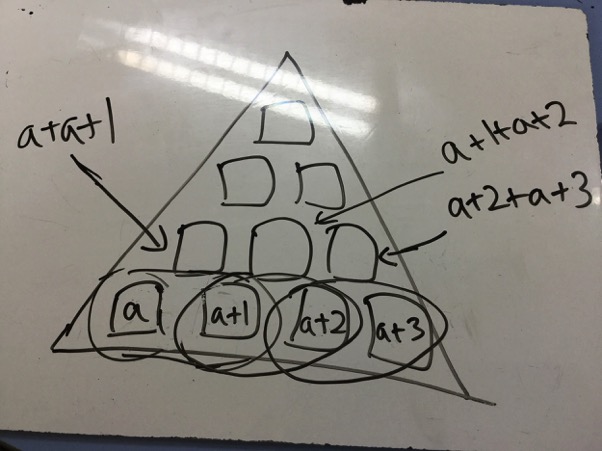
Simplyified:
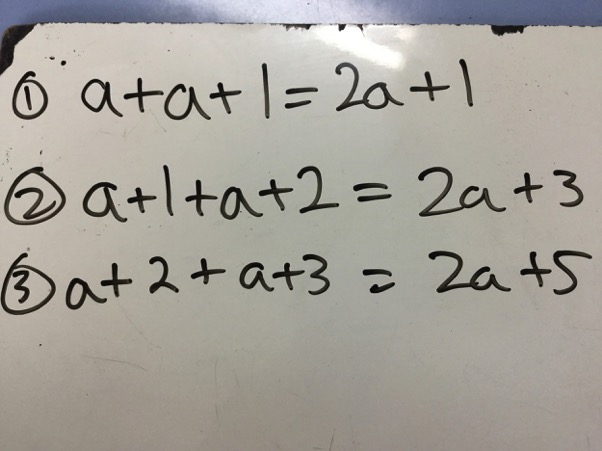
So the next layer would be
$2a + 1 + 2a + 3$ and $2a + 3 + 2a + 5$
Simplified:
$2a + 1 + 2a + 3 = 4a + 4$
$2a + 3 + 2a + 5 = 4a + 8$
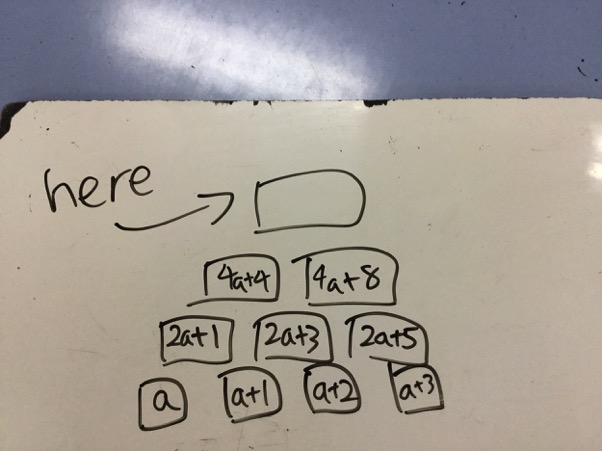
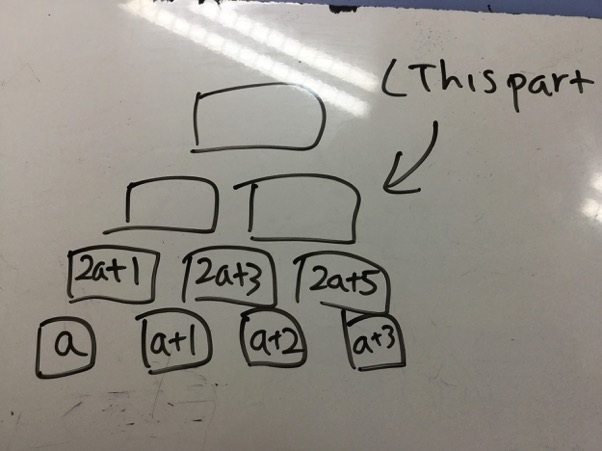
The last layer would be:
$4a + 4 + 4a + 8 = 8a + 12$
Can you use this method to explain why Leslie's method works?
Leslie thought of some numbers which will never go at the top:
0 will NEVER be at the top no matter what whole number is at the bottom. This is because since the pattern is ($a+b=c$) there is no way for two numbers in the same row to be the same, so you cannot get the number zero at the top (Leslie's method to find the top number was to add the four numbers on the bottom row and then double the answer). Also, decimals and fractions will never be at the top because you start with integers, so there is no way that a whole number going through the process will be at the top of the pyramid.
Maxim thought of some more:
It is impossible for odd numbers to appear at the top because if you add two evens together the product will always be even. We are adding a multiple of 8 (which cannot be odd) and 12 which must result as an even number.
In fact, the number at the top will always be a multiple of 4, but never a multiple of 8. Can you explain why?
Maxim and Leslie also found ways to find the bottom number from the top number. This is Maxim's method:
$(n-12)\div8$
I worked this out by doing the inverse of the first problem.
This is Leslie's method.
The way I found was to first subtract the top number by four, and then to divide the result by eight and then subtract one. For example, if you have 12 at the top of this pyramid, you can do twelve -four, and then divide by eight, getting 1. you subtract this by one, you get zero, the correct bottom left corner. This pattern does not work for decimals or if it goes by twos or threes.
Can you see why these two methods always give the same answer?
David from IES Maximo Laguna in Spain used algebra for pyramids with different step sizes. This is David's work:


