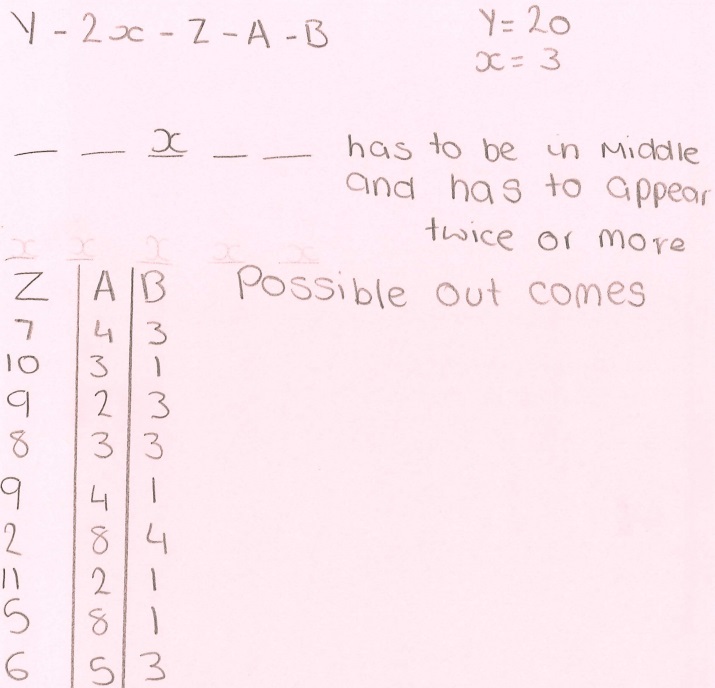Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
M, M and M



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to everyone who submitted a thoughtful solution to this problem, we received a large number. Along with many others, Sofia from Caxton College in Spain explained the conditions on the five numbers:
First you look at the mean. Imagine your mean is 4 and you have to give 5 numbers. So you multiply 4 by 5. Your product is 20. So your 5 numbers have to add up to 20 as when you divide them you will get the number 4.
If your median is 3 you have to make sure that the number 3 is in the middle of all the 5 numbers as they go in numerical order (_,_,3,_,_) .
Before the number 3 you have to have smaller number as it goes in numerical order e.g (2,3,3,_,_) and after the number three the numbers have to be
bigger (2,3,3,4,7). Now your median is 3 and your mean is 4.
If your mode is also 3 then all you have to do is assure that you use the number 3 more than other numbers. Like in my example I used the number 3 two times, and the rest, one time. So my mode is 3.
Using these ideas, Saanvi from the UK, Haoyang, Suhani and Zoe, Robert and Gabor from Garden International School in Malaysia, N from The Vine Inter-Church Primary School in the UK, Rafferrty, Ben and Javier from Twyford School, Winchester in the UK, Saanvi from Open Sky International in France, Connor from Shirley Boys High School in New Zealand, Niko from Mount Grace in the UK, Yuxin from St James Senior Girls School, Nikhil, Abhay and Ishaan from Ganit Kreeda, Vicharvatika in India and Anna from Caxton College all sent one or more sets of 5 numbers that meet the criteria. Here are some of their examples:
Ben: 2,3,3,3,9
Saanvi from Open Sky International:
1. Mean of given set of 5 whole number is 4 = 3, 3, 3, 5, 6
2. Median of the Same set 5 whole number is 3 = 3, 3, 3, 5, 6
3. Mode of Same set of 5 whole number is - 3 = 3, 3, 3, 5, 6
Connor:
1+3+3+5+8
3,3 mode
3, median
1+3+3+5+8=20/5=4
4, mean
Yuxin found these sets, as well as some of the ones above:
1,2,3,3,11
2,3,3,4,8
2,3,3,5,7
3,3,3,3,8
3,3,3,4,7
Nikhil found this sets, as well as some of the ones above:
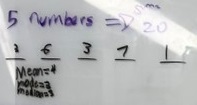
Suhani and Zoe found these sets, as well as some of the ones above:
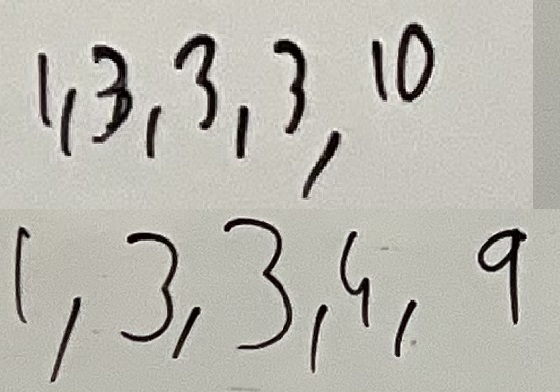
Lyla from CHS South expressed the numbers algebraically, and then found some possible sets. Here is Lyla's work (click on the image to open a larger version). Can you match Lyla's sets to the sets above?
Students from Farlingaye High School in the UK, Harry from St Michaels Preparatory School in Jersey, Arjun from Garden International School, Liam from Great Valley Middle School in the USA, Davie from Rugby School Thailand in Thailand and Iris and Lola from CHS South worked systematically by considering the possibilities for the smallest number. This is Harry's work:
I then organised the numbers so the number one would be in the first position, leaving the last two digits to add up to 13.
The same then happened when I started at 2 as the first number, but the last 2 digits added up to 12.
And when I tried with number 3, the end 2 digits added up to 11.
If I put 4 as the starting number, then 3 wouldn’t be used as the mode, for the mode goes in numerical order.
Solutions:
1 2 3 3 11
1 3 3 3 10
1 3 3 4 9
1 3 3 5 8
1 3 3 6 7
2 3 3 3 9
2 3 3 4 8
2 3 3 5 7
3 3 3 3 8
3 3 3 4 7
3 3 3 5 6
Nina W from Berlin Cosmopolitan School in Germany, Jon from The Old Priory School in the UK, Aniket from The ABC International School in Vietnam, Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia, Anathajith from Ganit Kreeda also worked systematically, by considering the positions of the 3s. This is Ananjith's work:
Suppose that when you arrange the five numbers in ascending order you get the number: a , b , c , d , e.
Case 1: c=3, d=3
a , b , c , d , e
| | | | | Only Possibility for this Case.
1 2 3 3 11
Case 2: b=3, c=3
a , b , c , d , e
| | | | |
1 3 3 6 7
1 3 3 5 8 5 Possibilities
1 3 3 4 9
2 3 3 5 7
2 3 3 4 8
Case 3: b=3, c=3, d=3
a , b , c , d , e
| | | | |
1 3 3 3 10 2 Possibilities
2 3 3 3 9
Case 4: a=3, b=3, c=3
a , b , c , d , e
| | | | |
3 3 3 5 6 2 Possibilities
3 3 3 4 7
Case 4: a=3, b=3, c=3, d=3 Only Possibility for this Case.
3 3 3 3 8
Note: The case where b, c, d and e are 3 is not possible because ‘a’ would have to be less than 3 and if it was, the sum wouldn't be 20.
Therefore, Total Number of possibilities = 1 + 5 + 2 + 2+1 = 11
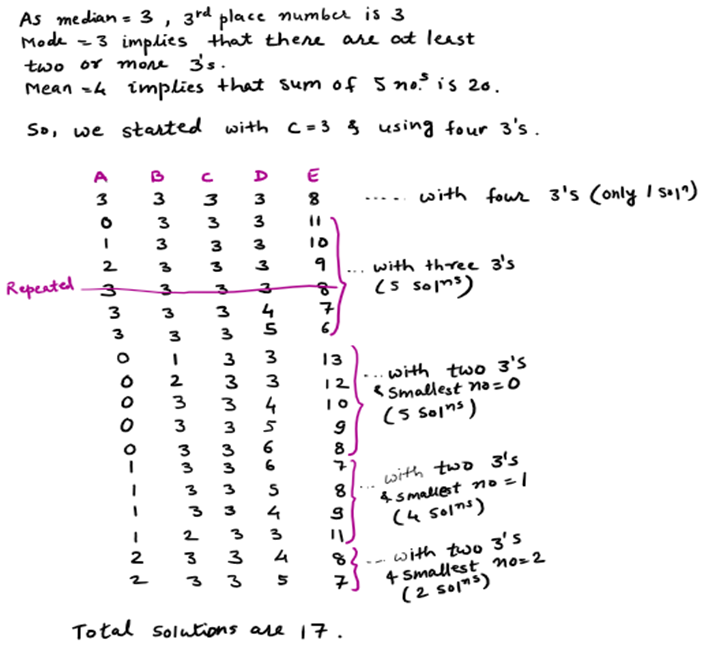
Naiana and Heidi from Rubgy School Thailand, Natalie from Bangkok Patana School in Thailand, Ira from Sahyadri School KFI in India, Mohammed from Repton School Abu Dhabi in the UAE, Shaunak from Ganit Manthan, Vicharvatika in India, Ahana from Ganit Kreeda, Avni and Sihun from Garden International School, Ahana, Ananthajith, Dhruv, Sehar, Saanvi, Nikhil, Insiya, Inaaya, Ishaan, Ishanvi, Sanat, Abhay, Karthik, Vishnuvardhan, Rudra from Ganit Kreeda, listed all the possibilities systematically based on the total number of 3s. This is Avni and Sihun's work:

This is the Ganit Kreeda students' woek from the entire group. They included 0 as a positive number, so they have more solutions:
Umar from Eastcourt Independent School in the UK wrote some Python code to find the possible sets. Here is Umar's code:
import random
# Using a set to store unique tuples
unique_triples = set()
for i in range(1, 100000):
num1 = random.randrange(1, 13)
num2 = random.randrange(1, 14 - num1)
num3 = 14 - num1 - num2
# Create a sorted tuple to avoid permutations of the same numbers
triple = tuple(sorted([num1, num2, num3]))
# Ensure all numbers are unique and the tuple is not already in the set
if len(set(triple)) == 3:
unique_triples.add(triple)
# Convert the set to a list if needed
unique_triples_list = list(unique_triples)
print(len(unique_triples_list))
print(unique_triples_list)
Can you work out what the code would output? Click to show an explanation.
Is it possible that any sets will be missed? For example, are there any cases where three of the numbers in the tuple could be the same?
Will the median always be 3?
Click to see Umar's investigation and conclusions based on the result of running the code:
Firstly, we need to prove the famous stars and bars and the n choose k function.
Imagine I have n cards, and I want to choose k of them but I do not care about the order in which I pick them. How many ways are there to pick k
cards. Well, I have n choices for the first card all the way down to k cards for the kth. This can be written as n!/(n - k)!. However, we overcount each one by k! as we did not consider that we do not care which order we pick them, so the new function is : n!/k!(n - k)!. This is known as the choose function.
Now imagine I have n stars and have k bars, such all bars have at least 1 star in them, and that the bars are labled but the stars are not. Now, instead of thinking of assigning the stars to the bars, think of assigning the bars to the stars by placing partitions between them. Here, we would need k-1 partitions. Also we have n-1 places to put them, as after every star except the last star. In other words I have n-1 valid solutions, and I have to place k-1 of them. This is n-1 choose k-1.
Now it is time to bring the proof together.If the length is five and the mean is 4, the sum of all the numbers must be 20. Also, if the mode is 3 there must be at least 2 instances of the number 3.This brings the total for the other numbers down to 14. If we think of there being 14 stars and the bars being the three numbers, we get the total number of solutions being 78. However, a portion of them contain duplicates of a number which we cant have, as then the mode would not be 3.Also, this includes duplicates of the same sets but in a different order. To remove the sets with multiple numbers, not that there can not be 3 duplicates as 14 is not a multiple of 3 . Think of the first number being n. Then, the folowing numbers are (14 - n)/2.This means n is an even number, as otherwise the duplicates will not be a whole number. There are 6 even numbers under 14. However, there are more sets than with duplicates because of the duplicate set problem. Sorry if the amount of duplicates confuse you! Convince yourself that there are 3 ways of rearranging a set with 2 duplicates. Then, there are 18 sets with a duplicate taking that out from 78, we get 60. As there are n! ways to rearrange a set with no duplicates for length n, this brings the amount of sets down to 10.However we are missing one out: the 3, 3, 8 solution. This was counted out because it had a duplicate, but as three is the duplicate number is 3, this is a valid set. Therefore, the total distinct ways of a valid set is 11, which is what my program said.
Footnote:
Thanks for such an intresting problem: I came up with the proof at night like I usually do. I haven't encountered such a nice problem for a long time, and it is nice to put the thereoms I know to use. Couldn't thank you more!
James from Norwich School in the UK posed and answered another question:
I found a way to make a set of 5 numbers with the same mean mode median and range as long as it is even.