Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Mind Your Ps and Qs



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Isaac from Glenthorne High School and Pratyush from Wilson's School in the UK, Amelie from Jersey College for Girls and Dylan who all sent in mostly correct solutions - especially to those of you who did some extra research to make sense of the $\iff$ and $\Rightarrow$ signs.
Click here to see Dylan's work, which includes Dylan's complete solution.
Isaac began:
First I labelled every statement chronologically A-O, and label the 16th statement R as P&Q are being used.

Pratyush and Amelie showed how they simplified some of the propositions, and they began matching as soon as they had simplified them. This is Patuyush's work for propositions B and K:

Note that it is not true that $x^2+x-2=0\iff x=1.$ Pratyush has already shown that $x^2+x-2=0\iff x=1\textbf{ or }x=-2.$
$x^2+x-2=0$ does not imply that $x=1,$ because $x$ could also be $-2.$ However it is true that $x=1\Rightarrow x^2+x-2=0.$
This is Amerlie's work for propositions A, F, I, M and R:
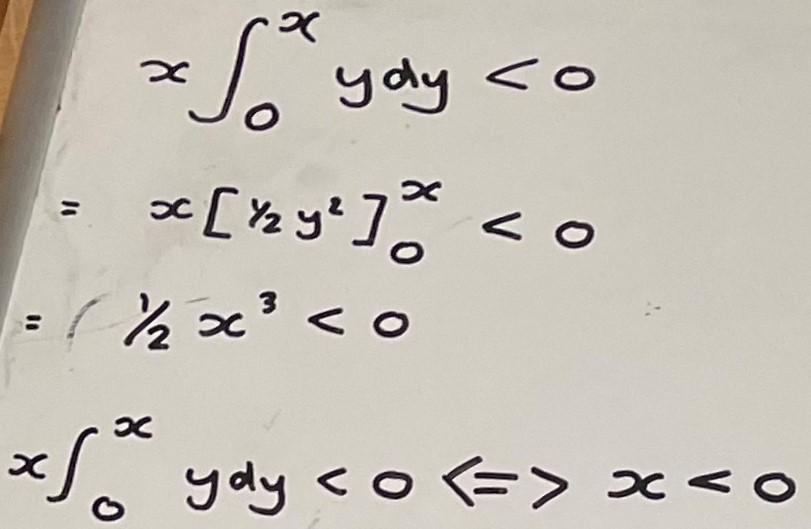
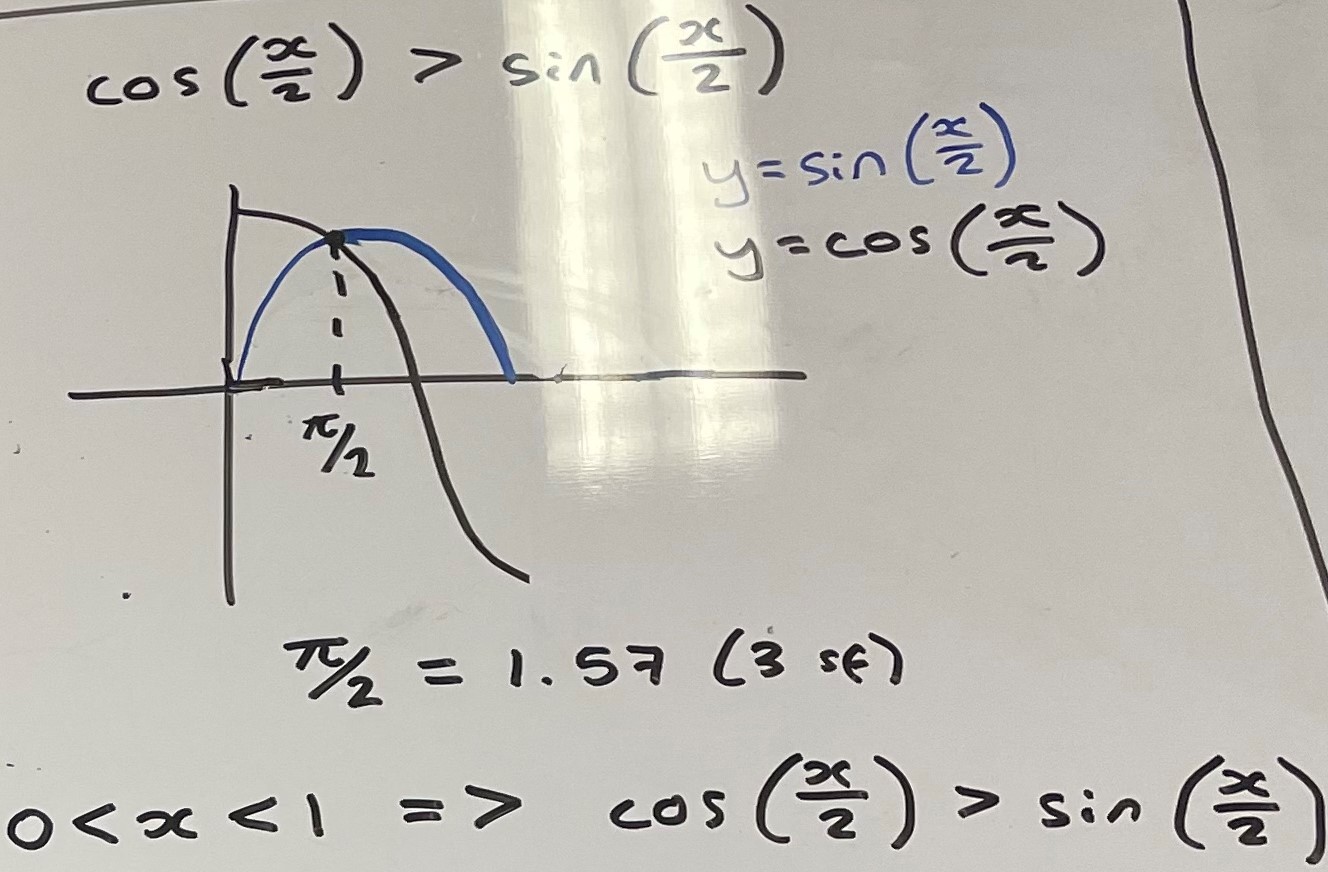
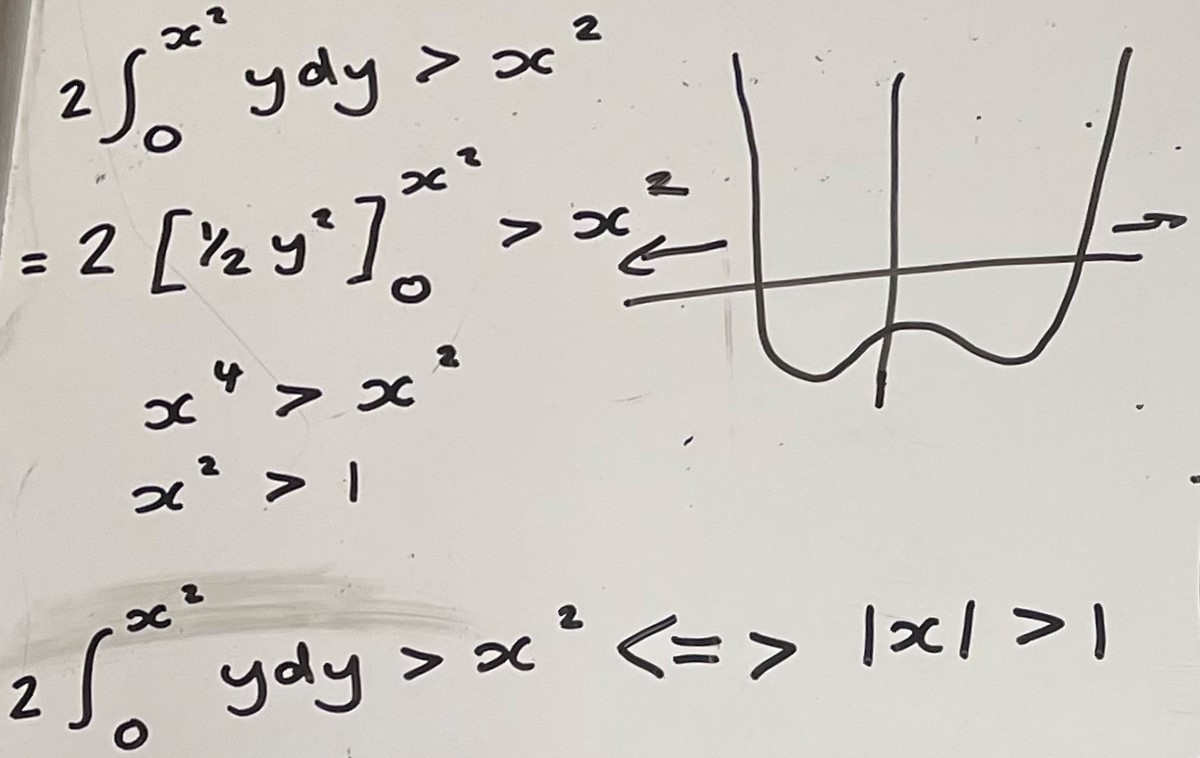
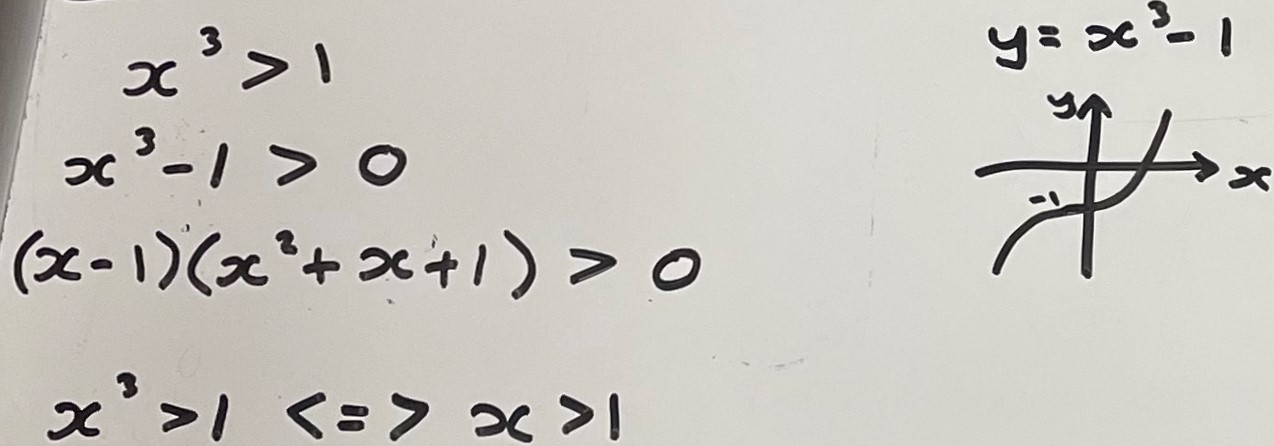
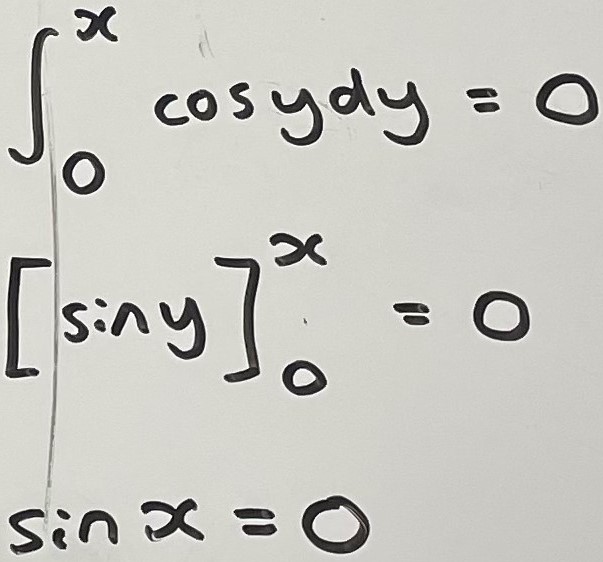
Amelie and Pratyush matched up as they went along, but Isaac used a more systematic approach (and Dylan's approach was the most systematc of all). Isaac wrote:
The only statement that was always true if A was true was J, so A$\Rightarrow$J. But if $x$ is less than $0$ then $\frac{x^3}2$ is less than $0,$ so I knew that A$\iff$J.
Repeat this process for every statement until all statements have a relationship with at least one other statement. Then I grouped together 4 $P\Rightarrow Q$ statements and 3 $P\iff Q$ statements, those being E$\Rightarrow$ R, H$\Rightarrow$K, L$\Rightarrow$F, O$\Rightarrow$G, A$\iff $J, B$\iff $M and I$\iff $N. With this we're left over with C and D, which have no shared value of $x$ thus no $P\Rightarrow Q$ or $P\iff Q$ relationship.
I focused on C, and found that the only relationship C is in with any other statement is C$\Rightarrow$F, so I replaced L$\Rightarrow$F with C$\Rightarrow$F, and compared the leftover statements L & D. L states that $x = -2,$ which is the only root to D's equation, therefore L$\iff$D, and now every statement is in a pair with 4 $P\Rightarrow Q$ relationships and 4 $P\iff Q$ relationships,
that being:
E$\Rightarrow$R, H$\Rightarrow$K, C$\Rightarrow$F, O$\Rightarrow$G,
A$\iff$J, B$\iff$M, I$\iff$N and L$\iff$D.

