Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Marbles in a Box



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Joel and Sarah from Sawston Village College, and Ethan from North Cross in New Zealand, found alternative methods for working out the number of different winning lines in a $3 \times 3 \times 3$ cube. Here is the description of Joel and Sarah's method. Ethan's method is shown below. Congratulations! Finding all the lines once, and none of them twice, is a real challenge.
 We can first treat it as a 2 dimensional tic tac toe game, just with 3 layers. Since there are 8 winning lines in a 2D game, and there are 3 layers, we can treat it like there are 3 different boards, each with 8
solutions. 3x8 = 24.
We can first treat it as a 2 dimensional tic tac toe game, just with 3 layers. Since there are 8 winning lines in a 2D game, and there are 3 layers, we can treat it like there are 3 different boards, each with 8
solutions. 3x8 = 24.
 Next, we look at the 3D model. Since we can have one nought/cross in one layer, one in another layer, and one in the final layer, this gives us a winning line (that is, a winning line which goes diagonally upwards from the bottom layer to the top
layer). This means we can convert it into a 2D board: when viewed from above, each of these sloping winning lines looks like a winning line on a flat board. However, top to bottom and bottom to top are different winning lines, and both look the same from above. This gives us 2 winning lines for every 2D winning line.
Next, we look at the 3D model. Since we can have one nought/cross in one layer, one in another layer, and one in the final layer, this gives us a winning line (that is, a winning line which goes diagonally upwards from the bottom layer to the top
layer). This means we can convert it into a 2D board: when viewed from above, each of these sloping winning lines looks like a winning line on a flat board. However, top to bottom and bottom to top are different winning lines, and both look the same from above. This gives us 2 winning lines for every 2D winning line.
Therefore, 8 regular solutions for a regular tic tac toe board x2 = 16.
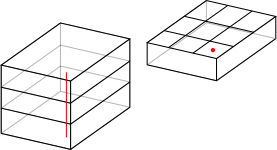 Finally, there are 3 layers, which means that we can have for example the top left for the top, top left for the middle, and top left for the bottom. This applies with every square on a regular tic tac toe board. There are 9 squares, so there are 9 more winning
lines.
Finally, there are 3 layers, which means that we can have for example the top left for the top, top left for the middle, and top left for the bottom. This applies with every square on a regular tic tac toe board. There are 9 squares, so there are 9 more winning
lines.
24+16+9 = 49 winning lines.
The second part of the problem asked if it was possible to adapt the methods described for the $3 \times 3 \times 3$ cube to give a general formula for any size cube.
Jamal from King Edward VII School, Sheffield managed to adapt Caroline's method to a $4 \times 4 \times 4$ cube.
Remember that on a $3 \times 3 \times 3$ cube all winning lines must pass either:
- along an edge of the cube
- through the middle of a face
- through the centre of the cube
but these must be changed to make it work for a $4 \times 4 \times 4$ cube.
There are still 12 edges on a $4 \times 4 \times 4$ cube so there are 12 winning lines along edges.
Since on the larger cube there is no 'middle' of a face, I counted all the lines on each face that aren't along the edge instead, each one passes through the 'middle' four pieces of a face. There are 2 diagonals, 2 horizontal and 2 vertical lines on each of the 6 faces, so that's 36 more lines.
Again the $4 \times 4 \times 4$ doesn't have a 'centre' piece so I counted all the lines through the central $2 \times 2 \times 2$ block. I found there is exactly one winning line through any two of those eight pieces in the block. There are (8x7)/2 =28 pairs because I can choose from eight pieces for the first one, then from the remaining seven for the second, but I divide by two because it
doesn't matter in what order I choose at the pair.
Adding these up I have 12 + 36 + 28 = 76 winning lines.
Niharika used similar reasoning to find the number of winning lines in an $n \times n \times n$ cube.
Rachael from Lancaster Girls' Grammar School used James' method to find the same result, and then generalised the answer to $n \times n \times n$ cubes.
Considering the non-diagonal winning lines first:
There are 16 from front to back.
There are 16 from left to right.
There are 16 from top to bottom.
Considering the diagonal winning lines:
On each layer there are 2 diagonal winning lines so:
There are 8 from front to back.
There are 8 from top to bottom.
There are 8 from left to right.
There are 4 lines from a vertex to a diagonally opposite vertex.
In total, there are 48+24+4 = 76 winning lines.
If I now take a cube of size nxnxn, there are n2 non-diagonal lines from front to back, and left to right, and top to bottom. That makes 3n2 lines. Counting the diagonal ones, there are 2 in each of the n layers, in each of the 3 dimensions; so 6n lines. Then there's the four lines from a vertex to a diagonally opposite vertex. In total there are 3n2 + 6n +4
lines.
Llewellyn from Cowbridge Comprehensive School saw that Alison's method generalises easily, jumping straight to the nxnxn formula.
A cube has 8 vertices, 12 edges and 6 faces. Correspondingly there are three kinds of pieces: vertex, edge, and face. An $n \times n \times n$ cube has 8 vertex peices, 12(n-2) edge pieces and 6(n-2)2 face pieces.
From a vertex piece there are 7 other vertex pieces that you can join to in order to make a winning line. 7×8 = 56 lines, but this counts each line from both ends, so there are 28 vertex winning lines.
From an edge piece there are 3 other edge pieces that you can join to in order to make a winning line. Remembering that this counts each line from both ends there are 3×12(n-2)/2 = 18n - 36 edge winning lines.
From a face piece there is one winning line, joining to the opposite face, so there are 6(n-2)2/2 = 3n2 - 12n + 12 face winning lines.
So in total, there are 28 + 18n - 36 + 3n2 - 12n + 12 = 3n2 + 6n + 4 winning lines. That means there are 76 winning lines in a 4x4x4 cube and 364 winning lines in a 10x10x10 cube.
Leah from St Paul's Girls' School saw how to adapt Grae's method to a solution for 4x4x4 cubes.
The winning lines may be counted by looking at lines:
- in each horizontal plane
- in each vertical plane from left to right
- in each vertical plane from front to back
- in the diagonal planes
On a non-diagonal plane there are 10 winning lines (4 horizontal, 4 vertical and 2 diagonal lines).
In the cube, there are 4 horizontal planes, so 10×4=40 winning lines.
There are also 4 vertical planes going from left to right, but now with only 6 new winning lines per plane, as the 4 horizontal lines have already been counted. So 6×4=24 winning lines.
On the 4 vertical planes going from front to back, we now only have 2 new (diagonal) winning lines per plane. So 2×4 = 8 winning lines.
Finally, there are also diagonal planes to consider. There are 4 winning lines going from corner to diagonally opposite corner.
In total, there are 40 + 24 + 8 + 4 = 76 winning lines.
It is possible to adapt Grae's and Caroline's methods to the general formula and you might like to try using Leah's or Jamal's work to help you get started. Of course it's easier now you know what formula you're looking for!

