Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Neighbourly Addition



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This task was used in one of our student webinars, thank you everyone who took part. During the webinar, we received 199 submissions. Some are included in the published solution, but to see all of them together, click here.docx
Oak Class from Bishopsdown explained why their answers were odd:
We have found out that when you add three odd numbers together the answer will always be odd. If you add two odd numbers together, the answer will be even for example, 1 + 3 = 4. If you then add another odd number to the total the answer will be odd e.g. 4 + 5 = 9.
6AT from Castle Academy noticed that:
...all answers are in the 3 times table
We discovered that adding 3 even numbers have the same result.
Taking this idea further, Max from Holy Trinity Pewley Down sent in this observation:-

Zara, Rizni and Mia from St. Christophers made the following observations:-
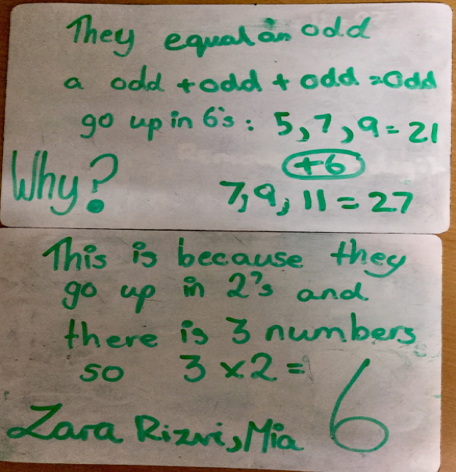
and Alvic and Sophie also from St. Christopher's added the following:-

Josh from Bignold Primary School wrote:-
When you have any amount of consecutive numbers (such as 3, 5 and 7) when you divide your number by the amount of numbers you have you get a whole number, for example, 3+5+7=15 15÷3=5 and 5 is a whole number. Also, that number can be classed as the 'middle number' as 5 comes between 3 and 7.
Saying you did the conjecture with a different set of numbers, such as 3, 5, 7 and 9, if you add the up (3+5+7+9=24), and then divided it by the amount of numbers (24÷4=6) you would get 6, which is a whole number and can be classed as the 'middle number' as it is between 5 and 7 .
Ashlyn Roy and Grace from St Christopher's Bahrain produced a simple algebra for the 3 houses:-

Louis from Olga Primary noticed something similar adding 5 consecutive houses:
When you add 5 odd numbers together the middle number always is the [middle number] times by 5.
I think this is because with each time the two numbers before taking away 4 and the 2 after adding four cancelling out the 4 before so you end up with the answer.
Children at Thorpe Primary in Peterborough produced a display of their work on this task. It includes some pictures which help to explain why the sum of three consecutive numbers is three times the middle number, and why the sum of five consecutive numbers is five times the middle number:

Shriya from The International School Frankfurt in Germany explained this using algebra:-
If I add five house numbers, the result would be 5 times the middle number
because -2 would cancel +2 and -4 would cancel +4.
E.g. 2+4+6+8+10=30
The middle number is 6.
6×5=30
This is the same with odd numbers.
If I add four house numbers, the result would be 4 times the average.
E.g.1+3+5+7=16
The average is 4.
4×4=16
This is the same with even numbers.
Siddharth from Village School, Princeton Junction, NJ, U.S.A also looked at more than 3 numbers and developed a rule:-
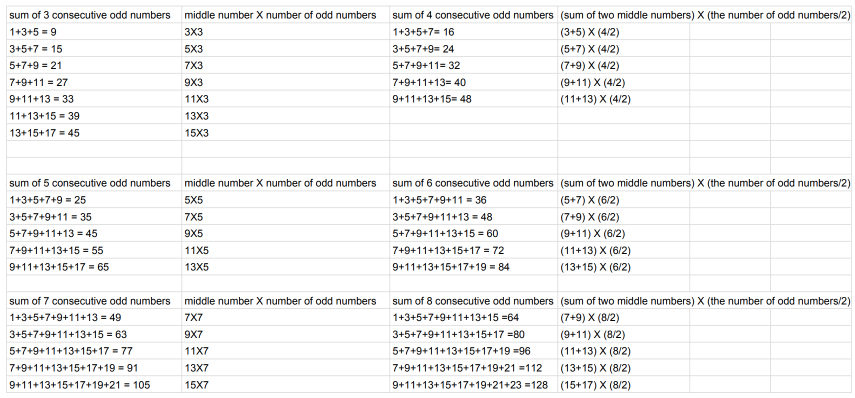
I started by listing consecutive odd numbers and adding them up in a spreadsheet. I started with 3 numbers, then 4 numbers, 5 numbers and so on. I started to see a pattern. The middle number (when there were odd number of numbers) or middle numbers (when there were even number of odd numbers) were important because I could find a rule using them. Please see below. I found that the rule was
middle number X number of odd numbers [when there were odd number of odd consecutive numbers] (sum of the 2 middle numbers) X (the number of odd numbers/2) [when there were even number of consecutive odd numbers]
Using the rule, I determined the sum of first 19 odd numbers
(1+3+5+7+9+11+13+15+17+19+21+23+25+27+29+31+33+35+37).
The middle number is 19, so 19 X 19 = 361. I then checked that my solution was correct by adding the 19 numbers using a calculator.
Using the rule, I determined the sum of first 20 odd numbers
(1+3+5+7+9+11+13+15+17+19+21+23+25+27+29+31+33+35+37+39). The middle numbers are 19 and 21, so (19+21)X(20/2) = 400. I then checked that my solution was correct by adding the 20 numbers using a calculator.
I then started a spreadsheet for 3 consecutive even numbers, 4 numbers and 5 numbers and so on. I saw that the even numbers followed the same rules as the odd numbers. I think it is because every consecutive odd number or consecutive even number is 2 numbers apart.
Frida and Jake from Colneis Junior School thought about the sequences made by the totals. This is some of Frida's work:

Jake also tried adding numbers with gaps other than 2:

David from LAET also used the sequences formed by the totals, and used them to find formulae for the sums of the house numbers. David's work includes:
- exploration of the sums of different numbers of house numbers
- a formula for adding $n+1$ house numbers
- a proof of this formula for even numbers (which uses sums of arithmetic sequences)
- two proofs of this formula for odd numbers (one using induction, one using sums of arithmetic sequences
- deducing the formula for gaps other than 2 (continuing Jake's idea above)
Click to see each of David's proofs.
David - exploration of the sums of different numbers of house numbers:
Sum of 2:
$n_0$: 1 3 5 7 9 ...
sum: 4 8 12 16 20 24 ... $(2n_0+2)$
Sum of 3:
sums: 9 15 21 27 33 ... $(3n_0+6)$
Sum of 4: 16 24 32 40 ... $(4n_0+12)$
Sum of 5: 25 35 45 55 65 ... $(5n_0+20)$
$\sum_{r=k}^{k+3}{2r+1} = 4(k+3) = 4k + 12$ (as given by the 'formula' for four numbers)
David - a formula for adding $n+1$ house numbers:
$$\sum_{r = k}^{k+n}{2r+1} = (n+a_0)(n+1)$$ where $a_0=2k+1$ is the starting point
"The sum of the first $n+1$ house numbers (odd) from the house numbered $a_0$"
And for even numbers:
$$\sum_{r = k}^{k+n}{2r} =(n+a_0) (n+1)$$
David's proof of this formula for even numbers:

David's proof of this formula for odd numbers using proof by induction:


David's proof of the formula without using proof by induction:
\\
&=\frac{k+n+1}{2}(1+(k+n)\times2+1)-\frac{k}{2}(2+(k-1)\times2)\\
&=(k+n+1)(1+k+n) - k(k+1-1)\\
&=(k+n+1)^2 - k^2\\
&=(k+n+1-k)(k+n+1+k)\\
&=(n+1)(2k+n+1)\end{align}$$ where $2k+1 = a_0$
My formula concludes that:
$\sum_{r=k}^{k+n}{2r+1} = (n+1)(n+a_0)$ where $n$ is a positive integer,
and
$\sum_{r=k}^{k+n}{2r} = (n+1)(n+a_0)$ where $n$ is a positive integer.
Note: $\sum_{r=k}^{k+n}{2r+1} = \sum_{r=k}^{k+n}{2r} \not\Rightarrow 2r+1 = 2r$
David's formula for gaps other than 2:

Thank you to those who took part in the successful webinar and for the submissions that came in afterwards.

