Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Factors and Multiples Puzzle



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This puzzle provides an interesting context which challenges students to apply their knowledge of the properties of numbers. Students need to work with various types of numbers at the same time and consider their relationships to each other (e.g. primes, squares and specific sets of multiples).
Possible approach
This printable worksheet may be useful: The Factors and Multiples Puzzle
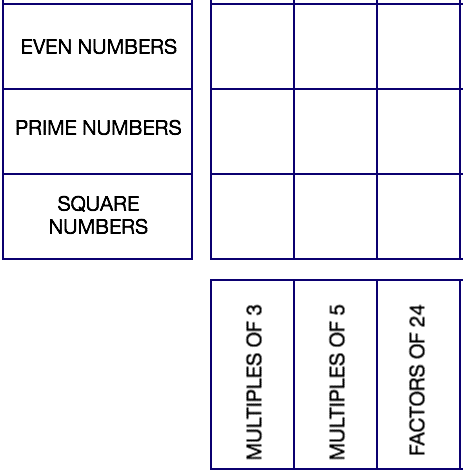
Show a $3 \times 3$ grid with six headings on the board, ask students to suggest numbers that could fit into each of the nine segments (an easy start, but useful revision of vocabulary).
The students (ideally working in twos or threes) can then be set the challenge of filling the $5 \times 5$ board with the available numbers. The challenge is to fit all 25 number cards onto the grid, so if they haven't been able to find a 'home' for all the number cards, suggest that they move some of the property cards around.
There is more than one possible solution so students could display their different arrangements. When a student/pair finishes allocating numbers to a grid, they should record the grid headings and how many numbers they placed.
A concluding plenary could ask students to share any insights and strategies that helped them succeed at this task.
A teacher comments:
Key questions
Which numbers are hard to place?
Encourage students to pay attention to the order in which they allocate numbers to cells - recognising the key cells to fill, and the key numbers to place.
Possible support
Some students could be given a larger range of numbers to choose from, or offered a smaller grid and appropriately restricted numbers - this could work with students choosing from the full set of $10$ categories, or with an adapted set.
Possible extension
Teachers can adapt the task by changing the heading cards or by asking students to create a new set of heading cards and a set of numbers that make it possible to fill the board. Students could then swap their new puzzles.
Is it possible to create a puzzle that can be filled with $25$ consecutive numbers?
Handouts for teachers are available here (word document, pdf document), with the problem on one side and the notes on the other.

