Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Different Deductions
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had quite a few solutions submitted for this task.
Oliver, Nicholas, Hayden, Elena and Iris, Jasmine and Dylan, Christie and Natalie from Peak School in Hong Kong said they mostly used 'guess, check and improve' to find the different values.
Henry from Winterfold House School sent in the following:
We chose a row that had three of the same shapes. We selected the highest FACTOR of the total for that row in place of the shape. Assuming the second shape was the difference between 3 times the first shape, we began to test and refine our solution using the other lines, columns and totals. circle=4; square=8; triangle=6 and hexagon=7
Tri from the British Vietnamese International School wrote:
This question is not hard or easy. My solution is to look at the first horizontal line and the two vertical lines from the right. You can see that:
2 square+ 2 triangle = 28, 3 square+1 triangle= 30.
You can say that the difference between 1 square and 1 triangle is 2.
So we have 28-2-2=24 because to make all the shape equal, 24 = 4 triangle so 1 triangle=6 and 1 square=8.
Now we can look at line 3 and 4 horizontal and we can see that 20 = 8 + 3c so circle = 4 and at line 3 vertically, we can have 23-4-4-8=7. so the? equals 7+4+4+6=21
Zara and Felicity from North London Collegiate Junior wrote:
In Maths Mayhem, our after-school maths club we solved this problem.
 A larger version can be viewed on a new page by clicking the image.
A larger version can be viewed on a new page by clicking the image.
Kavisin and Akshaya from Athelney Primary School wrote:
We worked this out in a systematic way. This is how we solved it:
We subtracted shapes and got some answers by looking at the totals of each column and row. We want to see if the numbers are greater or less than others. Then we knew that 2 squares plus 2 triangles = 28 and that means a square add a triangle = 14. We worked out that the difference between them was two and 14 -2 = 12. 12 divided by 2 is 6 so the triangle = 6 and the square = 8. When we knew that we worked out the other shapes and finally we found out the mystery number is 21!!!
Triangle plus Hexagon plus Circle plus Circle =21. 6 + 7 + 4 + 4 = 21
Freda from Meavy SchoolӬ sent in the following:
I found out that a square is two more than a triangle. Then I worked it out from there that a square must be 8 and a triangle must be 6. I then worked out a circle was 4 because there was a gap of 8, and there were two circles in the line. Finally, I looked at the value of a hexagon. I worked out that I needed 14 more to make the line with 2 hexagons and 2 squares. I knew that the 2 squares made 16 so that left 14 for the 2 hexagons. I split 14 and it made 7.
The final line was 7+6+4+4= 21.
Fred from Harris Primary Academy ShortlandsӬ said:
I started with the "30" column. This column has the same shape three times and one different shape. It adds up to 30. I thought "what number goes into 30 three times with a bit left over?" First I tried 9 for the orange square and 3 for the green triangle: 9+9+9 = 27, 27 + 3 = 30. Then I filled in the numbers that occurred there everywhere else. I tested it with the top row which adds up to 28. 3 + 9 + 9 + 3 = 24. So that can't be right!
Then I went back to my original column and tried some different numbers. 8+8+8 = 24, 24 + 6 = 30. So 8 and 6 would also work. I tried 8 and 6 in the top row and it worked: 6+8+8+6 = 28!
Once I had done this I could work out the bottom two rows with the red circles. The circle is worth the same in both rows, the only difference is that one row has a green triangle and one has an orange square. For the bottom row, I took away the number I already knew from the total: 20-8 = 12. I knew that 3 circles = 12 so 12 divided by 3 gives you one circle be 4.
Once you have three of the shapes you can work out the last one by adding down in the 23 column and working out what's left.
To get the answer I added all the answers to the shapes together. 6 + 7 + 4 + 4 = 21.
So the answer is 21.
Holy Trinity Pewley Down School sent in 3 solutions, click on the image
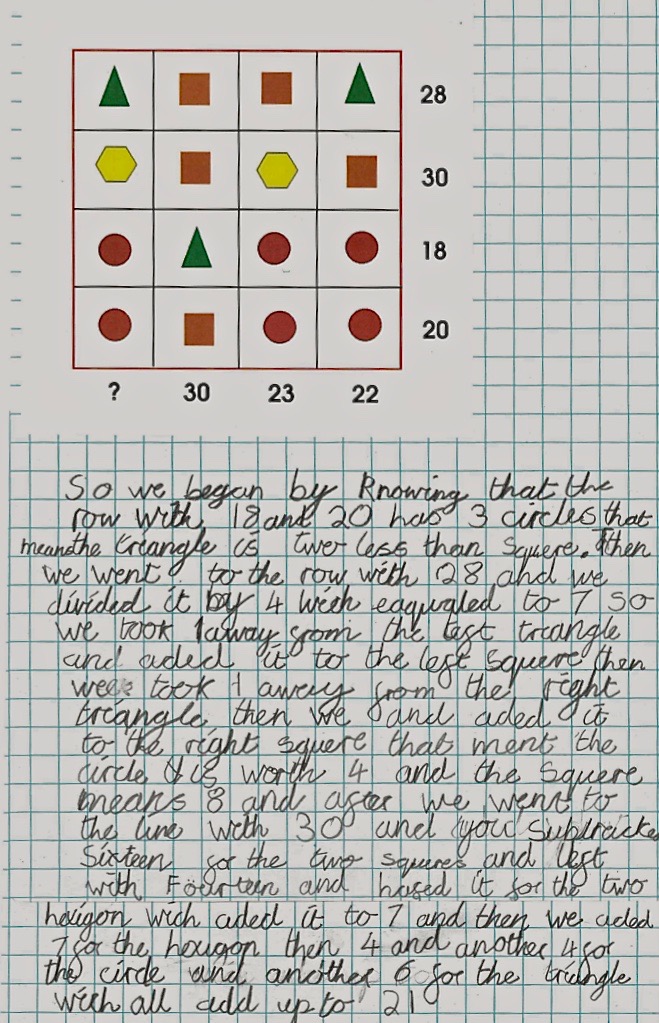

Florence from Walthamstow Hall Junior School wrote the following and there were other solutions from Gabby and Melissa:Ӭ
I started off by seeing what value some shapes had compared to others. The one you need to find out is the comparison between the square and the triangle. You can find this out by using the top 3rd and 4th rows or the top row and the 2nd column. For using the top row and the 2nd column: If 2 triangles+2 squares = 28. 1 triangle+3 squares= 30
When you substitute one of the triangles for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
For using the 3rd and 4th rows: If 3 circles + a triangle = 18, And 3 circles + a square = 20
When you substitute the triangle for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
Now you know that 1 square is 2 more than a triangle, this is how to figure out the exact value of the square and the triangle:
Again you use the top row and the 2nd column.
You know that 1 triangle + 3 squares = 30, so if you turn the triangle into a square by adding 2, the equation becomes 4 squares = 32. To find the value of a square, you divide 32 by 4 to make 32 ÷ 4 = 8. This means that a square's value must be 8. (To check this you can substitute two triangles into circles on the top row.)
Now that you know the value of a square and that a triangle is 2 less than a square, to find the value of a triangle you can do 8 - 2 = 6. Again you can check that this is correct by substituting shapes for numbers on the rows that only use squares and triangles.
To find the value of the remaining two shapes:
There are many ways to now find the value of the hexagon and the circle. The most obvious one is to:
1st use the 3rd and 4th rows to find the value of the circle.
If 3 circles + a square (8) = 20, just subtract the 8 from the 20 to make 20 - 8 = 12 and 12 ÷ 3 (representing the 3 circles) = 4. This 4 must be the value of a circle. (To check you can use the third row with a triangle rather than a square.)
To find out the value of a hexagon: (this is the easiest way, there are others)
Use the 2nd row. 2 squares + 2 hexagons = 30. 30 - 16 (2 squares) = 2 hexagons = 14
14 ÷ 2 (representing the 2 hexagons) = 7. This means that the value of a hexagon must be 7.
Overall values: Square = 8; Triangle = 6; Circle = 4; Hexagon = 7.
To find the missing value: A triangle + a hexagon + 2 circles = 6 + 7 + 4 + 4 = 6 + 7 + 8 = 21.
The missing value/answer is 21.
Thank you all for your contributions.
Oliver, Nicholas, Hayden, Elena and Iris, Jasmine and Dylan, Christie and Natalie from Peak School in Hong Kong said they mostly used 'guess, check and improve' to find the different values.
Henry from Winterfold House School sent in the following:
We chose a row that had three of the same shapes. We selected the highest FACTOR of the total for that row in place of the shape. Assuming the second shape was the difference between 3 times the first shape, we began to test and refine our solution using the other lines, columns and totals. circle=4; square=8; triangle=6 and hexagon=7
Tri from the British Vietnamese International School wrote:
This question is not hard or easy. My solution is to look at the first horizontal line and the two vertical lines from the right. You can see that:
2 square+ 2 triangle = 28, 3 square+1 triangle= 30.
You can say that the difference between 1 square and 1 triangle is 2.
So we have 28-2-2=24 because to make all the shape equal, 24 = 4 triangle so 1 triangle=6 and 1 square=8.
Now we can look at line 3 and 4 horizontal and we can see that 20 = 8 + 3c so circle = 4 and at line 3 vertically, we can have 23-4-4-8=7. so the? equals 7+4+4+6=21
Zara and Felicity from North London Collegiate Junior wrote:
In Maths Mayhem, our after-school maths club we solved this problem.

 A larger version can be viewed on a new page by clicking the image.
A larger version can be viewed on a new page by clicking the image.Kavisin and Akshaya from Athelney Primary School wrote:
We worked this out in a systematic way. This is how we solved it:
We subtracted shapes and got some answers by looking at the totals of each column and row. We want to see if the numbers are greater or less than others. Then we knew that 2 squares plus 2 triangles = 28 and that means a square add a triangle = 14. We worked out that the difference between them was two and 14 -2 = 12. 12 divided by 2 is 6 so the triangle = 6 and the square = 8. When we knew that we worked out the other shapes and finally we found out the mystery number is 21!!!
Triangle plus Hexagon plus Circle plus Circle =21. 6 + 7 + 4 + 4 = 21
Freda from Meavy SchoolӬ sent in the following:
I found out that a square is two more than a triangle. Then I worked it out from there that a square must be 8 and a triangle must be 6. I then worked out a circle was 4 because there was a gap of 8, and there were two circles in the line. Finally, I looked at the value of a hexagon. I worked out that I needed 14 more to make the line with 2 hexagons and 2 squares. I knew that the 2 squares made 16 so that left 14 for the 2 hexagons. I split 14 and it made 7.
The final line was 7+6+4+4= 21.
Fred from Harris Primary Academy ShortlandsӬ said:
I started with the "30" column. This column has the same shape three times and one different shape. It adds up to 30. I thought "what number goes into 30 three times with a bit left over?" First I tried 9 for the orange square and 3 for the green triangle: 9+9+9 = 27, 27 + 3 = 30. Then I filled in the numbers that occurred there everywhere else. I tested it with the top row which adds up to 28. 3 + 9 + 9 + 3 = 24. So that can't be right!
Then I went back to my original column and tried some different numbers. 8+8+8 = 24, 24 + 6 = 30. So 8 and 6 would also work. I tried 8 and 6 in the top row and it worked: 6+8+8+6 = 28!
Once I had done this I could work out the bottom two rows with the red circles. The circle is worth the same in both rows, the only difference is that one row has a green triangle and one has an orange square. For the bottom row, I took away the number I already knew from the total: 20-8 = 12. I knew that 3 circles = 12 so 12 divided by 3 gives you one circle be 4.
Once you have three of the shapes you can work out the last one by adding down in the 23 column and working out what's left.
To get the answer I added all the answers to the shapes together. 6 + 7 + 4 + 4 = 21.
So the answer is 21.
Holy Trinity Pewley Down School sent in 3 solutions, click on the image



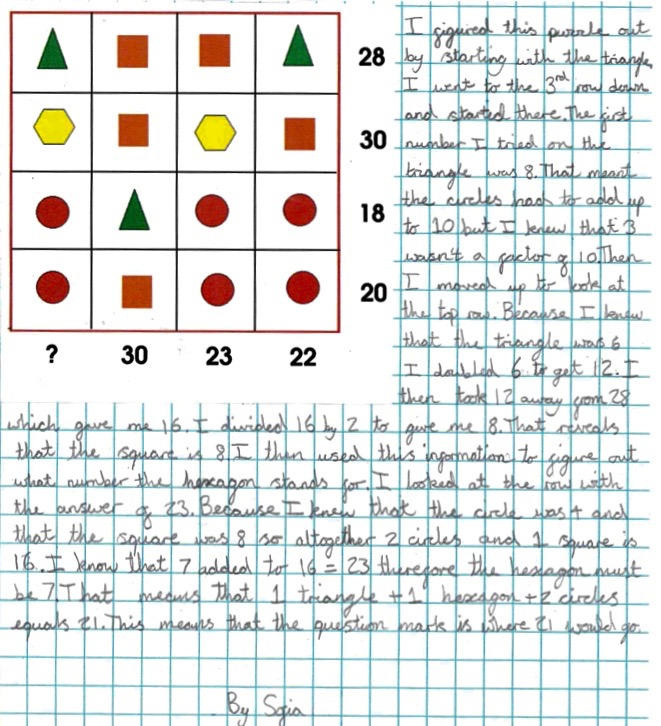
Florence from Walthamstow Hall Junior School wrote the following and there were other solutions from Gabby and Melissa:Ӭ
I started off by seeing what value some shapes had compared to others. The one you need to find out is the comparison between the square and the triangle. You can find this out by using the top 3rd and 4th rows or the top row and the 2nd column. For using the top row and the 2nd column: If 2 triangles+2 squares = 28. 1 triangle+3 squares= 30
When you substitute one of the triangles for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
For using the 3rd and 4th rows: If 3 circles + a triangle = 18, And 3 circles + a square = 20
When you substitute the triangle for a square, the total increases by 2. This means that 1 square must be 2 more than a triangle.
Now you know that 1 square is 2 more than a triangle, this is how to figure out the exact value of the square and the triangle:
Again you use the top row and the 2nd column.
You know that 1 triangle + 3 squares = 30, so if you turn the triangle into a square by adding 2, the equation becomes 4 squares = 32. To find the value of a square, you divide 32 by 4 to make 32 ÷ 4 = 8. This means that a square's value must be 8. (To check this you can substitute two triangles into circles on the top row.)
Now that you know the value of a square and that a triangle is 2 less than a square, to find the value of a triangle you can do 8 - 2 = 6. Again you can check that this is correct by substituting shapes for numbers on the rows that only use squares and triangles.
To find the value of the remaining two shapes:
There are many ways to now find the value of the hexagon and the circle. The most obvious one is to:
1st use the 3rd and 4th rows to find the value of the circle.
If 3 circles + a square (8) = 20, just subtract the 8 from the 20 to make 20 - 8 = 12 and 12 ÷ 3 (representing the 3 circles) = 4. This 4 must be the value of a circle. (To check you can use the third row with a triangle rather than a square.)
To find out the value of a hexagon: (this is the easiest way, there are others)
Use the 2nd row. 2 squares + 2 hexagons = 30. 30 - 16 (2 squares) = 2 hexagons = 14
14 ÷ 2 (representing the 2 hexagons) = 7. This means that the value of a hexagon must be 7.
Overall values: Square = 8; Triangle = 6; Circle = 4; Hexagon = 7.
To find the missing value: A triangle + a hexagon + 2 circles = 6 + 7 + 4 + 4 = 6 + 7 + 8 = 21.
The missing value/answer is 21.
Thank you all for your contributions.

