Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cyclic Quadrilaterals



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
Possible approach
You can print out 9-point Circles for students to work on, or use the GeoGebra applet.
"Draw as many different triangles as you can, by joining the centre dot and any two of the dots on the edge. Can you work out the angles in your triangles, if you know the 9 points are equally spaced around the circle?"
Give students some time to think on their own and then ask them to discuss their ideas with their partners. Then bring the class together and invite students to explain and justify how they calculated each angle.
"We've worked out some angles in triangles, now let's think about quadrilaterals"
"I'd like you to draw some different quadrilaterals by joining four of the nine points around the circle (cyclic quadrilaterals), and then use what you know about angles to work out the angles at the four vertices."
To start with, you may wish students to only draw examples where the centre of the circle lies inside the quadrilateral.
While students are working, you could display an image like the one below to offer a hint for how to work out the angles in the quadrilateral:
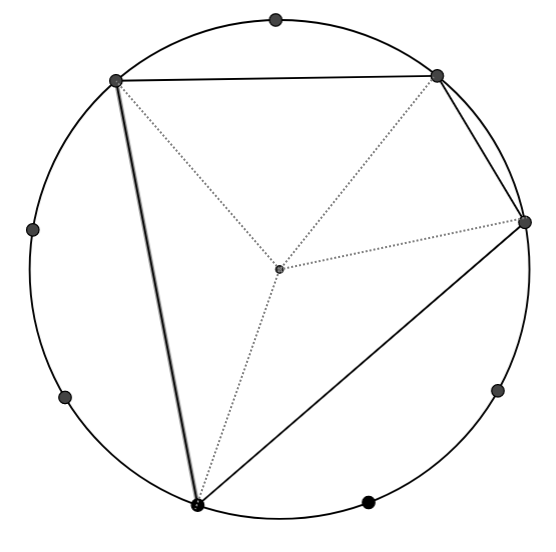
Once everyone has had a chance to draw some quadrilaterals and work out the angles, bring the class together and ask a few students to read out the four angles going around one of their quadrilaterals, and draw a table on the board to collect the results. It might look something like this:
| Angle A | Angle B | Angle C | Angle D |
|---|---|---|---|
| 140 | 60 | 40 | 120 |
| 100 | 80 | 80 | 100 |
| 120 | 100 | 60 | 80 |
| 80 | 140 | 100 | 40 |
“Take a look at the table. What do you notice?”
Give students a little thinking time, drawing attention to pairs of columns A and C, and B and D, if no suggestions are forthcoming.
“It looks as though the opposite angles add up to 180 degrees! I wonder if the same would happen if we used circles with more than 9 points?”
This might be a good place to stop, if you're planning to use this task over several lessons.
Hand out 10 dot, 12 dot, 15 dot and 18 dot circles, and invite different groups of students to draw quadrilaterals, work out the angles, and
add their results to the table on the board. Once there is a good deal of evidence, bring the class together again.
“Well we haven't found any examples where the opposite angles don't add up to 180 degrees, but that doesn't mean it will always work - I wonder if we can prove it?”
"Will the same happen if you draw a circle and choose four points at random to form a quadrilateral?" - see Possible extension below.
Possible support
Triangles in Circles eases students in a bit more gently to exploring angles on a 9-point circle.
Possible extension
To prove that the opposite angles of all cyclic quadrilaterals add to $180^\circ$ ask students to take a look at Cyclic Quadrilaterals Proof
Students could be challenged to think about cyclic quadrilaterals where the centre of the circle is not contained within the quadrilateral.
Other circle theorems could be explored in a similar way - see Circumference Angles, Subtended Angles and Right Angles.

