Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cuboids
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
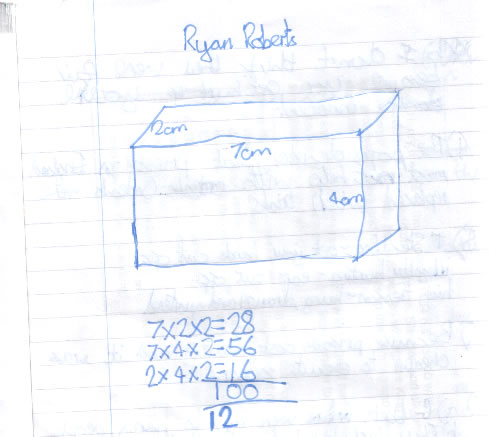
Steven and Ryan found that a 2x4x7
cuboid has a surface area of 100 square units.
Justin from Mason Middle School found that a 1x2x16 cuboid also satisfies the conditions:
I back it up by saying that$1\times 2 = 2$,
$2 \times16 = 32$
and $16 \times1 = 16$
and add them all up and you get $50$, and then multiply by $2$ and you get a square area of $100$!
Megan was able to show that these were the only two possible solutions:
Call the lengths of the 3 dimensions (height, depth, width) $x$, $y$ and $z$.The surface area is $2xy+2xz+2yz$, as the area of each face is calculated by multiplying its two sides together, and there are $2$ of each face.
Hence, $2xy+2xz+2yz = 100$.
Dividing by $2$, $xy+yz+xz = 50$.
I will assume that $x$ is the shortest side and $z$ the longest to avoid repeating solutions. Therefore I must find integer solutions to the equation $xy+yz+xz = 50$ where $x < y < z$.
Rearranging the equation,
$yz+xz = 50-xy$
$z(x+y) = 50-xy$
$z = (50-xy)/(x+y)$.
I used an excel spreadsheet with 3 columns, 1 for each of $x$, $y$ and $z$.
In the $z$ column I write the rearranged formula.
I then started from $x = 1$, $y = 1,2,3...$ looking for integer values of $z$ until I reached a solution which had been repeated (as here $y$ is bigger than $z$, so I would be repeating values with $y$ and $z$ swapped around) or where $z$ became smaller than $y$.
For $x = 1$ I found only 1 solution, $(1, 2, 16)$.
Checking with the original formula this does agree to a total of $100$.
I then continued repeating the procedure with $x = 2$, $y = 2$,$3$,$4$... and found a solution of $(2, 4, 7)$.
With $x = 3$, $y = 3$,$4$,$5$... there are no solutions, as $z$ becomes smaller than $y$ where $y=5$ (and $z = 4.375$) and there are no integer solutions before this.
With $x = 4$, $y = 4,5,6...$ $z$ becomes smaller than $y$ when $y = 5$ $(z = 3.333)$ therefore there are no solutions where $x = 4$.
After $x = 4$, the intitial value of $z$ is always smaller than $y$, therefore there are no further solutions.
The only 2 solutions to the problem are: $(1, 2, 16)$ and $(2, 4, 7)$.
Fred from Albion Heights School also offered some non-integer solutions:
$h = 1$, $w = 1$, $l = 24.5$$h = 2$, $w = 2$, $l = 11.5 $
$h = 4$, $w = 4$, $l = 4.25$
$h = 2.5$, $w = 5$, $ l = 5$
$h = 1$, $w = 4$, $l = 9.2$
Well done to you all.

