Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Consecutive Numbers
- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
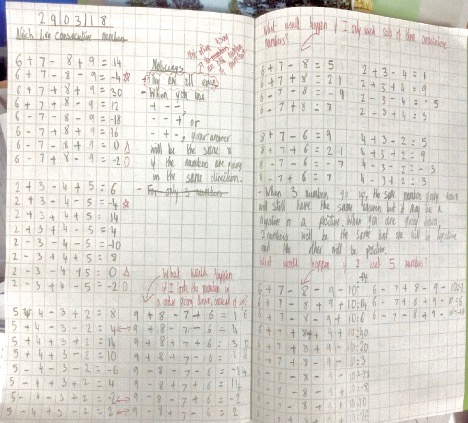
Kayley from Arnhem Wharf Primary School in London sent in this very good solution to the task:
When you use an even number of consecutive numbers, your answer will be even because there are two odd numbers and two even numbers in the equation. An odd number plus or minus another odd number equals an even number; an even number plus or minus an even number equals an even number; therefore the two answers (odd +/- odd and even +/- even) are even numbers and if you add it all together it will still be an even number.
I noticed that if you use the sequences +--, --+ or -+- with four consecutive numbers, your answer will be the same, no matter what consecutive numbers you use, if both sets numbers are ordered in the same way (e.g. from smallest to biggest). A set of three consecutive numbers will have odd answers if the starting number is even because an even number add or subtract an odd number will be odd, then when you add or subtract another odd number the answer will be odd.
I also found out that if there is a set of three consecutive numbers, and the starting number is odd, all the answers will be even because an odd plus/minus an even number is odd and if you plus/minus an odd number, the answer will be even.
These pictures show her work, the red writing being her thoughts. Larger versions can be viewed here: First page and Second page

Iris, Hannah, Hayden and Tawana from Fenstanton and Hilton Primary School said:
We worked out the calculations for 1, 2, 3, 4 as our consecutive numbers. These are the calculations we worked out:1+2+3+4= 10; 1+2+3-4= 2; 1+2-3-4= -4; 1-2-3-4= 4;
1-2-3+4= -2; 1-2-3-4= -8; 1-2-3+4= 0; 1-2+3+4= 6
Are you surprised by anything you noticed? We noticed that all the numbers are even, which would make sense because if you are adding consecutive numbers there will always be two odd numbers and two even, which means they will always add up to an even number.
What would happen if you had the numbers going in descending order instead of ascending order? We found out that when we put the numbers in descending order they were all still even and that some of the numbers were there same but mostly different.
We got:
4+3+2+1=10; 4+3+2-1=8; 4+3-2-1=4; 4-3-2-1=-2
4-3-2+1=0: 4-3+2+1=4; 4+3-2+1=6; 4-3+2-1=2
James and Polly from the very small Meavy CE Primary School sent in this excellent solution:
Our answer to the consecutive numbers challenge:
30-31-32-33=-66 and 30+31+32+33=126 are some of the questions only using adding and subtraction using the numbers 30, 31, 32, 33. You can only get eight different calculations:
1. + + +; 2. + + -; 3. + - +; 4. + - -
5. - + +; 6. - + -; 7. - - +; 8. - - -
We found out that the answers you always get are 0, -2 and -4 using - - + (in any order).
If you put something in the middle of the eight answers, once you have put them in order, the gap between the answers will be like a mirror image.
We did the problem four times so that we could make sure that our answer was right. These were the groups of numbers we used:
| The numbers we started with | The eight answers | The gaps between the answers |
| 1,2,3,4 | 10,6,4,2,0,-2,-4,-8 | 4,2,2,2,2,2,4 |
| 7,8,9,10 | 34,18,16,14,0,-2,-4,-20 | 16,2,2,14,2,2,16 |
| 20,21,22,23 | 86,44,42,40,0,-2,-4,-46 | 42,2,2,40,2,2,42 |
| 30,31,32,33 | 126,64,62,60,0,-2,-4,-66 | 62,2,2,60,2,2,62 |
James thinks that the middle number in the gaps is double the start number and the outside numbers are double the second number. Polly thinks the middle number in the gaps is double the start number but the outside numbers are double the first number and add two. Both of our suggestions are right.
Mrs Bromley a teacher at Skelton Primary School, York sent in Joseph's work, saying,
This morning we really enjoyed investigating consecutive numbers using your resource.
She remembered that Joseph said:
I decided to investigate odd and even numbers. I was surprised that even amounts of numbers give an even answer. I predicted that using three consecutive numbers would always give odd answers but I was proved wrong! Next, I would like to look at what happens if you start with an odd or even number.
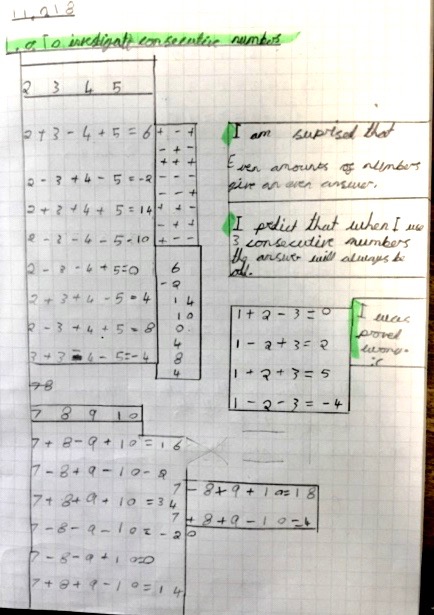

You can see Joseph's work more clearly as .jpg files here and here.
Thank you all for these really helpful solutions which may encourage others to pursue the same task.



