Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
American Billions



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We have received solutions from Emily and Ellie from Fitzharrys School, Victor from St. Paul's in Brazil, Jack from Springwood Academy, Rebecca from Loughborough High School, Komal from Alexandra School in India, Sam, Nathan and Dan from Netherthong Primary School, Anurag from Queen Elizabeth's Grammar School in Horncastle, Tom, Jake, Harry and Michael from Corsham Primary School, George from Onslow St. Audrey's School, Ali from Riccarton High School in Christchurch, New Zealand, and Luke from Cottenham in Cambridgeshire.
Victor found that 12365 could be made a little longer:
Yes, 123654 is divisible by 6, but they can't go any futher than that.
He had a go at finding the longest number you can make that satisfies the rules of the game. He managed a seven digit number:
7836542 is my attempt, I didn't manage to use all of the digits.
Jack found a six digit number that satisfied the rules:
147258
Emily & Ellie found a seven digit number:
9632581
It is possible to find a ten digit number that satisfies the rules. It is:
3816547290
since
3 is divisible by 1
38 is divisible by 2
381 is divisible by 3
3816 is divisible by 4
38165 is divisible by 5
381654 is divisible by 6
3816547 is divisible by 7
38165472 is divisible by 8
381654729 is divisible by 9
3816547290 is divisible by 10
Tom, Jake, Harry and Michael worked it out like this:
We realised that the 0 had to go at the end (Units) for it to be a multiple of 10.
We then knew the 5th number would have to be a 5 - because it's the only other multiple of 5.
We realised that any number divisible by 2 , 4, 6 or 8 had to be an even number.
From this we decided the billion digit must be odd and the following digits even and so on:
We used the elimination method starting with 98 and went down to 92 and kept on going down. Eventually we found the answer: 3816547290.
Ali worked it out like this:
Let A B C D E F G H I J represent the 10 digits.
The number itself is divisible by 10, so J must be 0.
Since the number formed by the first 5 digits from the left is divisible by 5, E must be 5 or 0, but since we have used 0 already, E must be 5.
Since AB, ABCD, ABCDEF and ABCDEFGH must be divisible by 2, 4, 6 and 8 respectively, they must all be even. Therefore B, D, F and H must be even numbers.
That leaves 1, 3, 7 and 9 for A, C, G and I.
Ali then started listing the possible combinations, and eliminating those that did not fit:
AB could be any of the following:

The number formed by the first 3 digits from the left is divisible by 3, so the digits must add up to a number that is divisible by 3.
The possible values of ABC can now be identified:
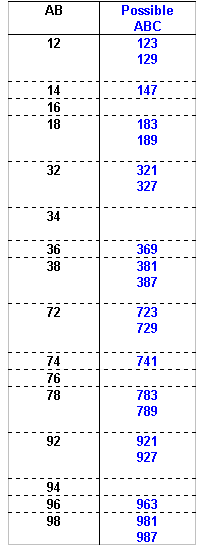
The number formed by the first 4 digits from the left is divisible by 4, so the number formed by the last two digits of the number must also be divisible by 4 (since all multiples of 100 are divisible by 4 we can ignore the digits in the hundreds and thousands column).
The possible values of ABCD can now be identified:
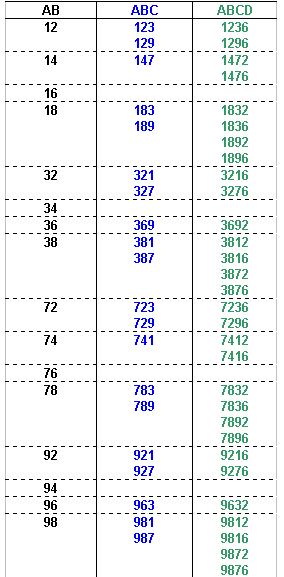
We know that the fifth digit must be 5, so the possible values of ABCDE can now be identified:
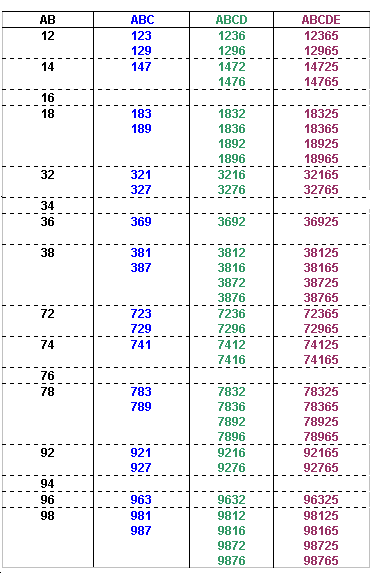
The number formed by the first 6 digits from the left is divisible by 6, so it must be even, and the digits must add up to a number that is divisible by 3 (since it must be a multiple of 3).
The possible values of ABCDEF can now be identified:
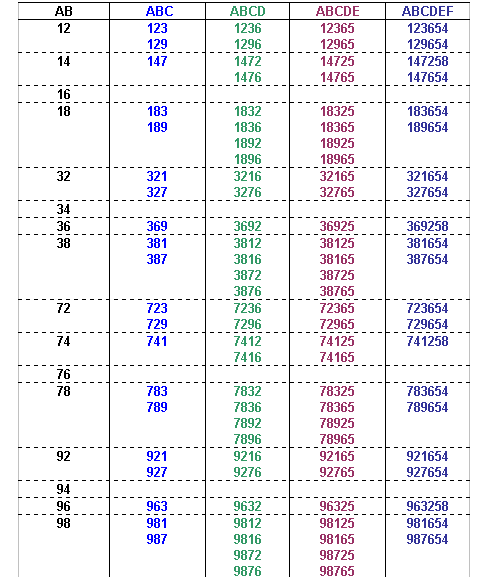
The number formed by the first 7 digits from the left is divisible by 7, and the seventh digit must be odd.
The possible values of ABCDEFG can now be identified:
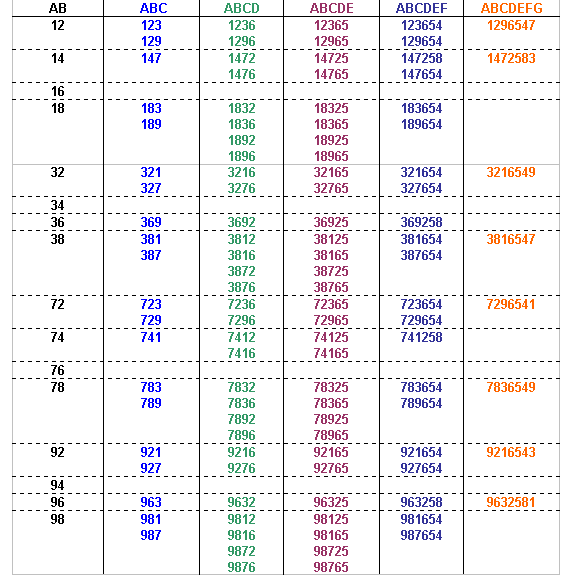
The number formed by the first 8 digits from the left is divisible by 8, so the number formed by the last three digits of the number must also be divisible by 8 (since all multiples of 1000 are divisible by 8 we can ignore the digits in the thousands, ten thousands and hundred thousands column).
That leaves only one option for ABCDEFGH:
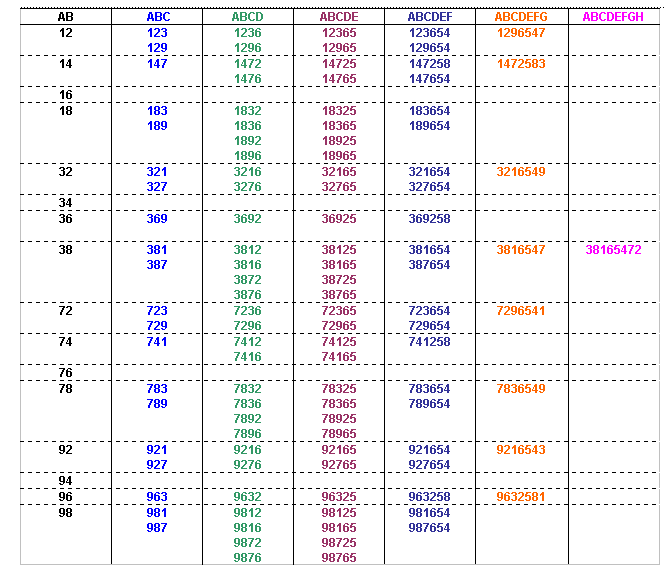
Therefore ABCDEFGHIJ can only be:
3816547290
Here is Anurag's solution.
Luke explained his reasoning like this:
I knew that the last digit was zero because only numbers that have zero at the end are divisible by ten.
xxxxxxxxx0
Numbers that are divisible by 5 end in 5 or 0, and 0 has already been used so the fifth digit must be 5.
xxxx5xxxx0
Since an odd number is not divisible by an even number, the pattern must go odd, even, odd, even,..
The second digit is even and, since multiples of 100 are divisible by 4, the number formed by the first 4 digits from the left will be divisible by 4 if the number formed by the last two digits is divisible by 4,
so, ignoring the first two digits,
we know that the fourth digit has to be 2 or 6 since 14, 34, 74, 94, 18, 38, 78 and 98 are not divisible by 4. (The third digit must be odd, and not 5).
So these are our options:
xxx25xxxx0
xxx65xxxx0
The sixth digit is even and, since multiples of 200 are divisible by 8, the number formed by the first 8 digits from the left will be divisible by 8 if the number formed by the last two digits is divisible by 8,
so, ignoring the first six digits
we know that the eighth digit has to be 2 or 6 since 14, 34, 74, 94, 18, 38, 78 and 98 are not divisible by 8. (The seventh number must be odd, and not 5).
Since the fourth digit must be 2 or a 6 as well that means that the second and sixth digits must be 4 or 8.
So these are our options:
x4x258x6x0
x4x658x2x0
x8x254x6x0
x8x654x2x0
This is the bit my Dad helped with. The sum of the first 3 digits must be divisible by 3. Also the sum of the first 6 digits must be divisible by 3. Therefore the sum of the fourth, fifth and sixth digits must be divisible by 3.
So these are our options now:
x4x258x6x0
x8x654x2x0
The first 3 digits must add up to 3.
This gives us the following options:
147258x6x0
741258x6x0
183654x2x0
381654x2x0
189654x2x0
981654x2x0
789654x2x0
987654x2x0
Because the sixth digit is even, and the eighth digit is either 2 or 6,
we can can only have 16, 32, 72, or 96 for the seventh and eighth digits (they are divisible by 8),
and these numbers can't have been used elsewhere.
The ninth digit can be anything because the sum of all the digits 1 to 9 is divisible by 9.
This gives us the following options:
1472589630
7412589630
1836547290
3816547290
1896543270
1896547230
9816543270
9816547230
7896543210
9876543210
Finally, if we check that the numbers formed by the first 7 digits from the left are divisible by 7, we find that the only possible answer is
3816547290
Rebecca also found 3816547290. She sent us this explanation:
We can immediately say that the last digit has to be 0 because the whole number has to be divisible by 10.
The 5th digit:
The 0 has already been used, excluding the chances of the 5th digit being anything other than 5, as the 5th digit has to be divisible by 5.
Even and Odd:
We can also figure out that the 2nd, 4th, 6th, and 8th digits have to be even because no multiple of 2, 4, 6 or 8 can be odd. This means that the 1st, 3rd, 5th, 7th and 9th digits must be odd!
The 4th and 8th digits:
Any hundred can be divided by 4 so we have to focus on the 3rd and 4th digits. In the 4 times table, after every odd ten comes a 2 or a 6. For example: 32, 76, 52, 96 etc?
We therefore know that digit 4 can only be 2 or 6, and because 8 is double 4, this rule applies to the 8th digit too.
This also means that the 2nd and 6th digits can only be 4 or 8.
What next?
After this, the quickest method is to use trial and error, in a structured manner, starting at either the smallest or largest possible number.
Komal sent us this explanation, which demonstrates what a structured approach might look like:
Let our number be -
Also our 5-digit number should be divisible by 5. Hence E should be 0/5.
Each number comes only once and J is 0 therefore E will be 5.
Therefore B, D, F and H are even numbers i.e. 2, 4, 6, 8.
Sam, Nathan and Dan used the rules for divisibility they knew:
The first rule did not help us so we ignored it.
We knew that rule 10 would be 0 and rule 5 would be 5.
Rule 2 would be even.
To figure out rule 3 add all the digits together and if the digital root is 3,6 or 9 it is divisible by 3.
Rule 4 must be even and the last 2 has to be divisible by 4.
Rule 6 add all the units together and if it is divisible by 3 and the full number is divisble 2 it is right.
Rule 7 use one of the odd numbers that is left.
Rule 8 has to be even and the last 3 digits must add up to be divisible by 8.
Rule 9 just use the last digit that is left or add all the digits up and if that is divisible by 9 the number is divisble by 9 and then add a 0.
Your answer should be 3816547290. Good luck!!!!
George also used the rules for divisibility he knew:

