More Christmas Boxes
Problem
Start with a $10$ by $10$ grid.
If you cut out each corner square, it could be folded into an open-top box that had an $8$ by $8$ base and was $1$ square deep. That means that the box would be able to hold $64$ cubes.
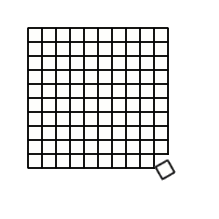
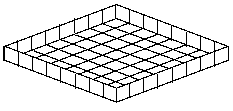
What size square should you cut out of each corner to make the
box that would hold the greatest number of unit cubes?
(Another way to ask this question is 'Which box has the greatest
volume of space available?'.)
Student Solutions
Jason from Priory School, Dunstable says:
"If you cut 2 squares deep it will become a 6 x 6 base which I make as the biggest amount of space: 72 cubes. I worked this out using :
Length x Width x Height
6 x 6 x 2 = 72"
Christina (Marborough Primary, London) and Josh (Ampthill, Bedfordshire) agree with this answer.
Josh said, "At first I thought it would be best to cut out a 3x3 square at each corner, but that box only held 48 cubes. If you cut out a 2x2 square though, the box will hold 2x6x6 cubes which is 72. That is the most."