Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Making Cuboids



Let's say you can only use two different lengths - $2$ units and $4$ units.
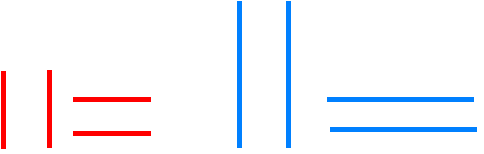
If you are using these lengths to make the sides of rectangles, how many different ones can you make? (Squares are just special rectangles!)
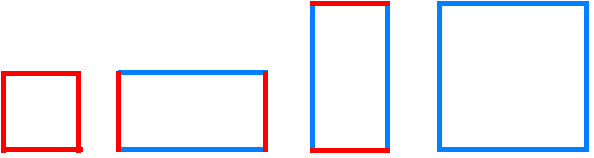
There are three because two are the same - just rotated.
But we are not making $2$-dimensional rectangles!
We are going to make $3$-dimensional cuboids.
Using just these two lengths as the edges of the cuboids how many different ones can you make?
Here are two of them. How many more are there?
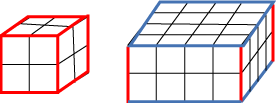
It is a good idea to make them from squared paper and sticky tape, but you also need to find a way to record your results.
This is one way to show the results above, making a list.
| The smallest is | $2 \times 2 \times2$ |
| The middle sized one is | $2 \times4 \times4$ |
You should find a way to record your results that makes sense to you.
How can you make sure that your cuboids are not the same if rotated?
How many different cuboids did you get?
But what if we have three different lengths: $2$ units, $3$ units and $4$ units?

How many different cuboids can you make now?
Make them from squared paper and sticky tape.
Remember to record your results.
Find a way of showing what they look like.
Once they are made perhaps you can arrange them in order of size - but how will you work this out?

