Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Arsenal Collection: Stadium Sightline



- Problem
- Getting Started
- Teachers' Resources
Why do this problem?
This problem encourages students to model a real-life situation mathematically, that of tiered seating design in sports stadia. The problem begins with some straightforward geometry but leads into some spreadsheet modelling. Although the problem can be solved using trigonometry, the most elegant solution simply uses similar triangles.
Possible approach
"Your task is to design the seating layout for the stadium. The seats will be tiered so that the back of each seat is 80cm behind the back of the seat in front, but raised up so that each row can see over the row in front. Start by making some sketches of how you think the seats might need to be arranged."
Give students time to try out some ideas. Perhaps sketch on the board (or invite students to sketch) a variety of possibilities - straight lines of different gradients, and convex and concave curves. Then allow some time for students to share their intuitions about which will best model a successful tiered seating design, together with any reasons they have to support it.
Next, introduce the diagram:
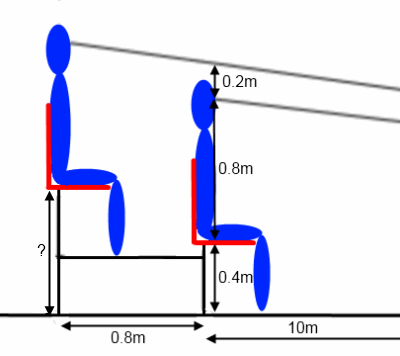
Set the next task, to work out the missing height. Students may wish to draw or plot accurate diagrams before making calculations.
Move on to working out the height above ground level of the third seat, and allow some time to discuss whether students are surprised that the extra height is not constant.
Finally, invite students to explore what happens for subsequent steps, perhaps using spreadsheets to iterate and calculate the next step height from the previous.
Key questions
What sort of a view would spectators have if each seat was higher than the one before by the same distance?
What sort of a view would spectators have if the angle between their line of sight and the line of sight of the spectator in front was constant?
Possible extension
Invite students to consider other factors that might affect stadium seating and perhaps adapt their models accordingly.
Possible support
Track Design looks at a simpler design context at the Olympics.

