Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Magic Constants



- Problem
- Teachers' Resources
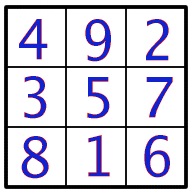
Magic Constants
This is a 4 x 4 Magic Square made from the numbers 1 to 16.

In a Magic Square all the rows, columns and diagonals add to the same number. This number is called the 'Magic Constant'.
Here are some questions about this Magic Square.
1/What is the Magic Constant of this Magic Square?
This particular square is especially 'magic' as some 2 x 2 squares within it also add to that number.
2/How many of these squares can you find?
3/What happens to the Magic Constant if you add 2 to each number in the square?
4/What happens if you double each number?
5/Can you make a square in which the Magic Constant is 17?
7/What other numbers under 100 can you make into the Magic Constant by changing all the numbers in the square in the same way?
8/Can some be made in more than one way?
9/Are there some numbers you really cannot make?
Why do this problem?
Possible approach