You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Three Way Split
Take any point P inside an equilateral triangle. Draw PA, PB and PC from P perpendicular to the sides of the triangle where A, B and C are points on the sides. Prove that PA + PB + PC is a constant.
Age 14 to 16
Challenge Level
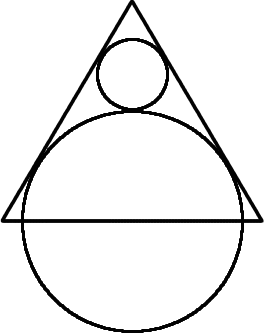
The centre of the larger circle is at the midpoint of one side of an equilateral triangle and the circle touches the other two sides of the triangle.
A smaller circle touches the larger circle and two sides of the triangle.
If the small circle has radius 1 unit, find the radius of the larger circle.
NRICH is part of the family of activities in the Millennium Mathematics Project.