Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Class 5's Names



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Class 5's Names
Here are the lists of first names of the members of Class $5$. (They are in alphabetical order of their surnames so they do not seem to be ordered.)
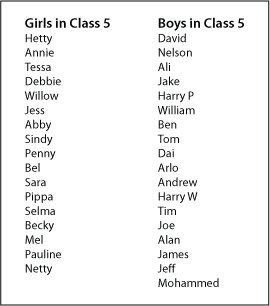
One day when $34$ children were in class, Mrs Clifton, their teacher, said they were going to make some block graphs and other things using their first names. She put the class lists onto the white board.
First, the class made tally charts of the initial letters of their names. They worked in pairs.
The first part of Becky and Selma's tally looked like this:

Can you make a full tally chart using the class names?
Next they all made frequency tables using this information.
This is the first part of Alan and Joe's table:
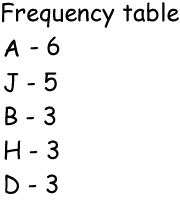
Can you make a frequency table using all the class's names?
Next they decided which letters of the alphabet were needed and which were not needed to make a block graph of their class names. Then the boys took yellow squares and the girls took pale blue squares, drew a picture of themselves and put the initial of their first name on the square and stuck it onto paper to make a pictogram graph.
The last part of the class's block graph looked like this:

Can you see who was away from school that day from this information?
Next they made true block graphs from the class lists to include anyone who was away that day.
This is part of the middle of the block graph:
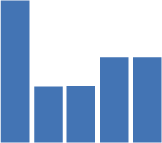
Can you tell what letters these were?
Can you make a block graph of all the class?
Why do this problem?
Possible approach
In a plenary, initiate discussion about how they knew which member of the class was away that day and encourage them to offer opinions on which of their representations is best for this data. Listen out for those that give clear explanations for their choices.
Key questions
Possible extension
The problem Real Statistics offers more opportunities for data analysis, and goes on to invite data collection and further analysis.
Possible support
The Pet Graph is a simpler challenge which focuses just on a block graph.

