Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Factorising with Multilink
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Luke from London Oratory School explained how the situation can be shown using algebra:
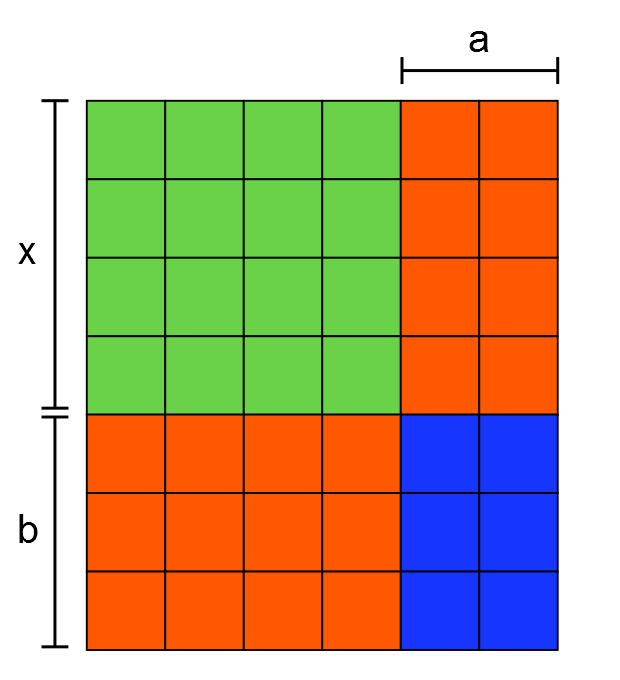
The red section (made of sticks) consists of two rectangles with dimensions $a, x$ and $b, x$. Therefore the red area is equal to $ax+bx$, which equals $x(a+b)$.
We can see that the area of the blue section will always have dimensions $a$ and $b$, so its area is equal to $ab$, if it Ê»ï¬llsʼ the gap created by the red area.
The total area is equal to the sum of these component areas.
Thus you can make a rectangle for all bases for expression of the form $x^2 + x(a+b) + ab$ where $a$ and $b$ are positive integers. The rectangle has dimensions $(x+a)$ by $(x+b)$.
1 square, lots of sticks and 12 or 100 units
Mahdi, Hamaad and Khalid used algebra again. Here is Mahdi's work for 12 sticks:
This is Hamaad and Khalid's work for 100 sticks:
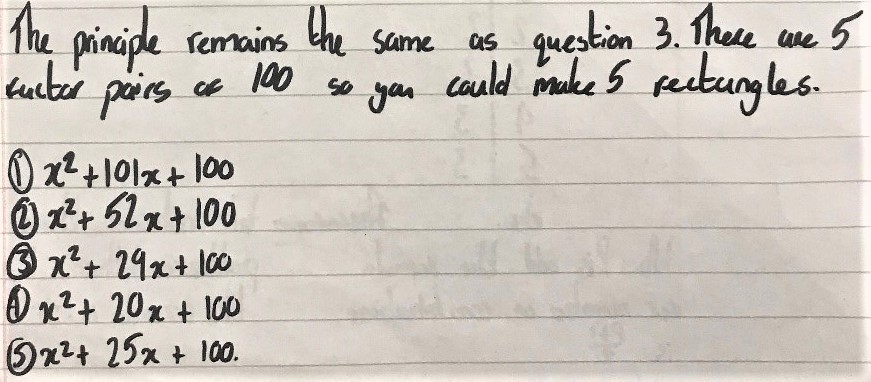
1 square, 12 or 100 sticks and lots of units
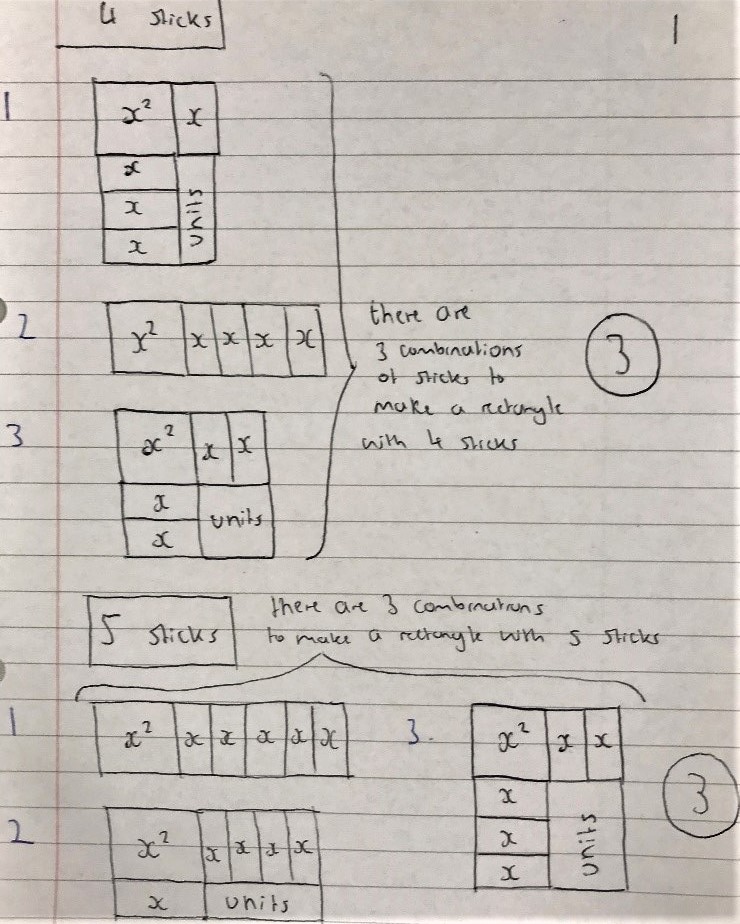
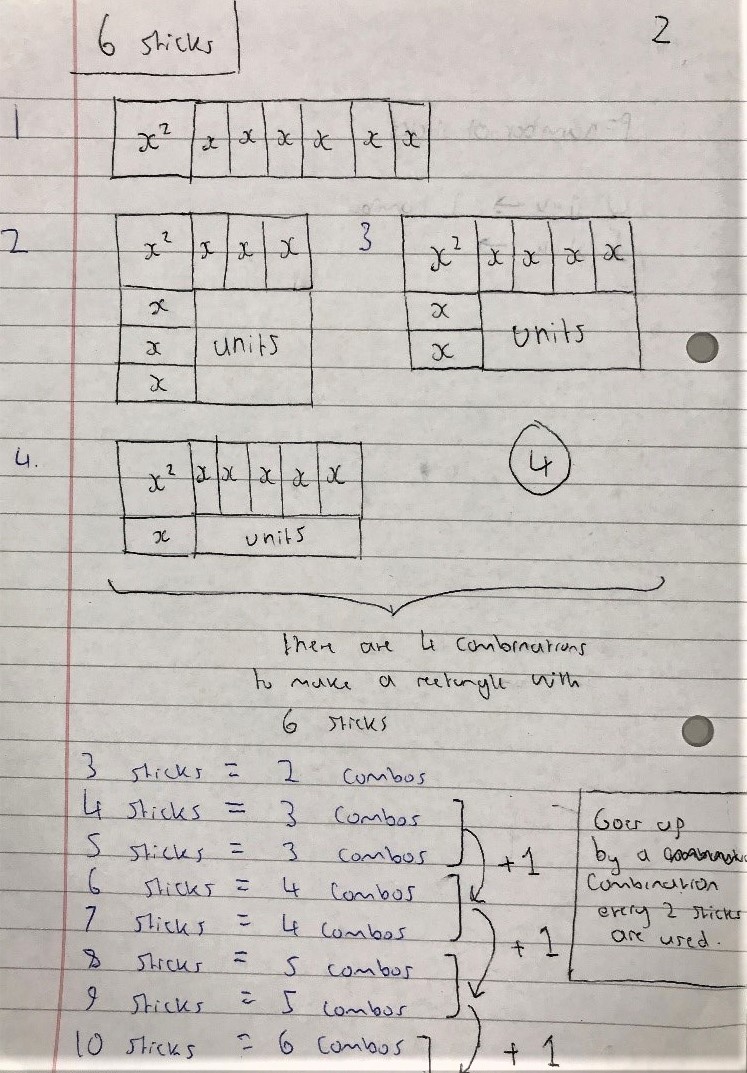
Hadi from Michaela Community School in the UK started with smaller numbers of sticks and then spotted a pattern:

Mahdi from Mahatma Gandhi International School in India used algebra:
Hamaad and Khalid from Michaela Community School and Mahdi used the same approah for 100 sticks. This is Hamaad and Khalid's work:

For $p$ sticks and $q$ units
Mahdi approached this algebraically:
So how many different rectangles can you make with $p$ sticks and $q$ units?