Those Tea Cups

Well done all of you who sent in these solutions. I am very pleased with the ways that you went about doing this challenge and the different ways you showed your results.

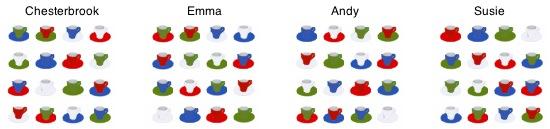
Pupils from Chesterbrook Academy sent in this,

We first started off by doing column by column and row by row. After we found out it would take us forever, we tried putting the doubles (green green, blue blue, etc.) in the middle four squares. This idea was given to us by our teacher, Mrs. Johnson. After that, we built off the center.
Our answers were:
First row
g r b w
b g w r

Second row
w b r g
g b r w

Third row
b w g r
r w g b

Fourth row
r g w b
w r b g

Then someone else from the same school added,

We figured it out by putting the doubles (white,white, green,green Etc.) in the middle. Then we put the ones that were opposites together and took each column too see if the patterns could go there. If it didn't work we switched the middle until we finally got it.

Here's Emma's Solution that she sent in in a doc.form:

Andy sent in the following. I liked his method for finding a solution by starting with the special diagonal and then filling in. I've not come across this method before. This solution has the added attraction (perhaps difficulty) that the diagonals also have to obey the rule!

The answer is
BB WR GW RG
RW GG WB BR
WG BW RR GB
GR RB BG WW

B stands for blue
G stands for green
R stands for red
W stands for white

The first letter of each double is the saucer
The second letter of each double is the cup

First we have to put the cups and saucers that are the same colour in a diagonal line. Then we work out the rest of the space by using the diagonal.
Eg BB GG
The space between BB and GG will be filled with RW and the opposite space would be filled with WR. In the end all the space would be filled in the the shape of a square and that is the answer.

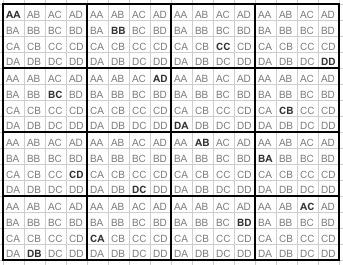
Susie sent in these comments accompanied by the Spreadsheet. This is the first time, out of hundreds of times, that I've been presented with this method of finding a solution.Well done Susie, (from Cathedral School, I wonder which one?).

I made a 4 by 4 square and wrote in each square pairs of letters AA, AB, AC to mean the colours of cups and saucers. I used Excel.
To select a cup and saucer I coloured the letters black and crossed the same thing off in all the other squares. If the thing I chose was AB then I would also cross off the A-somethings from same line and row, and I would also cross off the something-Bs from same line and row.
I started off by putting AA, BB, CC and DD on the top row. I wanted a diagonal going down right of A-somethings and a diagonal going down left of D-somethings.
In one square I had the choice of DA or DB so I chose one and carried on. I noticed a pattern of 2 short diagonals of C-somethings and B-somethings appearing. My dad helpd me with the spredsheet and with this email.

These four solutions could be viewed as:-