Phase Space

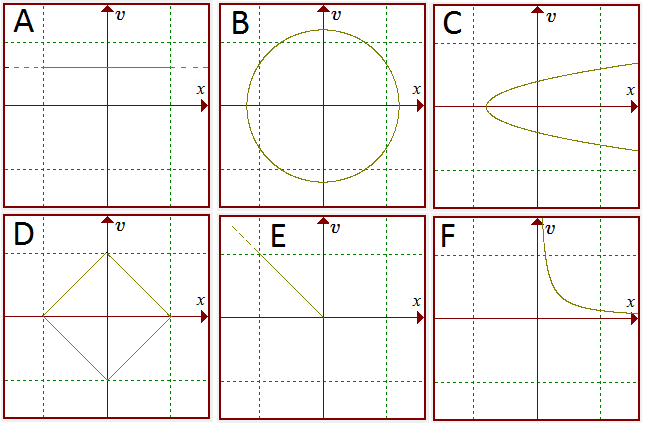
A particle moves in a straight line under the action of a unknown force and its motion is observed in various situations.

The position $x$ of the particle is plotted against its velocity $v$ for the motion in the following 6 cases.

In each case, what can you say about the motion of the particle?

In which way does each travel along the curve?

Can you think of a plausible physical interpretation for each?
 
What can you deduce about points corresponding to equal time intervals of the motion?



Next consider the velocity-position diagrams for the following situations:

1. A rubber ball dropped perpendicular to a hard concrete floor (if you know about coefficients of restitution, you could draw this motion accurately for $e=0.7$, neglecting all friction and air resistance)
2. A large parcel dropped from a stationary and very high helicopter.
3. An air hockey puck struck hard and perpendicular to a side on an air hockey table.


Extension: Think more generally about the meaning of velocity-position diagrams and the relationship to speed-time diagrams.