Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
L-triominoes
Age 14 to 16
Challenge Level 





A triomino is a shape made from three squares. Here is an L-triomino:

Here is a size 2 L-triomino:

It can be tiled with four size 1 L-triominoes:

Can you work out how to use the tiling of a size 2 L-triomino to help you to tile a size 4 L-triomino? Click here for a hint.
Devise a convincing argument that you will be able to tile a size 8, 16, 32... $2^n$ L-triomino using size 1 L-triominoes.
How many size 1 L-triominoes would you need to tile a size 8... 16... 32... $2^n$ L-triomino?
What about odd sized L-triominoes? The diagram below shows the region which needs to be tiled to turn a size 1 L-triomino into a size 3 L-triomino.
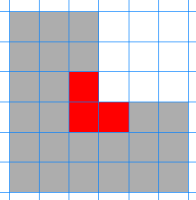

In the same way, can you find a way of adding to your size 3 tiling to tile a size 5? Then a size 7, 9, 11...? Click here for a hint.
Devise a convincing argument that you will be able to tile any odd sized L-triomino using size 1 L-triominoes.
Combine your ideas to produce a convincing argument that ANY size of L-triomino can be tiled.
Here is an interactive you could use to try out your ideas.