Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Rose
Age 16 to 18
Challenge Level 





|
1
 |
2 |
3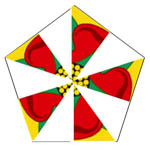 |
4 |
|
List the symmetries in each of the four diagrams, that is the
transformations which map the picture into itself.
What transformations do you get if you combine the
transformations from diagrams 3 and 4 in all possible ways?
A set of transformations, with the operation of combining
transformations, becomes a group when the set includes all possible
combinations of the transformations in the set.
Do the sets of transformations you have listed form groups
when their transformations are combined?
Can you find any other groups of transformations which map a
regular pentagon to itself?
How many distinctly different groups are there which map a
regular pentagon into itself?
Note: You don't need to do
more in order to submit a solution but why not pose some similar
questions for yourself? The article Paint Rollers for Frieze Patterns
explores in 3D the same idea of
groups of symmetries.
|

