Assessing Pupil Progress (APP) and NRICH Resources

Stage: 1, 2, 3, 4 and 5

Article by Jennifer Piggott

By Jenny Piggott

In the past many of us have tended to view mathematics in terms of content knowledge, whilst the new National Curriculum encourages us to think in terms of problem solving. In this article I suggest that there is a third dimension that is just as important to have in mind and is vital if we are to assess our pupils progress beyond their grasp of content knowledge.

The main questions for me are:

How can we identify progression in problem solving for planning and assessment purposes?
How can we make the most effective use of NRICH resources to support APP?

The rest of this article will address these questions.

A starting point

The main elements in the curriculum that we currently talk about are:

Mathematical content knowledge
Mathematical problem-solving skills (which include "key processes", "using and applying" and "mathematical thinking").

Resources on the NRICH website contain both these elements and some (such as those on the mapping documents) are particularly suited to addressing mathematical content knowledge through problem solving.

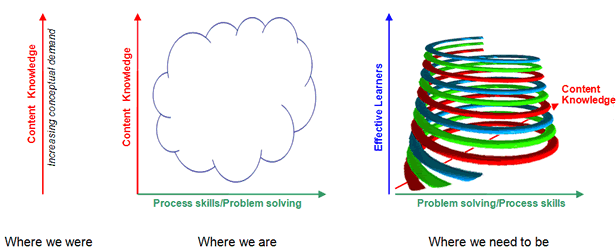
This means we have resources that fit together like this:

An important point to bear in mind is that whilst a problem normally requires all aspects of a learner's problem solving skills to be brought to bear, it will probably only cover a limited area of content knowledge (possibly one key concept or several concepts which come together and enable connections to be made). In any single context it is often possible to place different emphases on different aspects of process skills, such as representing or communicating, for making particular teaching or assessment points. However, it is almost impossible and generally undesirable to try to isolate process skills when problem solving.

With this model in mind we now want to look at what progression in process looks like and therefore what we should look for when assessing learners' process skills.

Thinking about progression in process

There is progression in mathematical process/problem solving. This progression lies within the experiences of the processes themselves. Processes are not a simple set of six (or so) things to do in a particular order and once you have done them you can "do" processes. Process skills are complex beasts, in terms of breadth, depth and diversity:

Different process skills can be used at different points as you problem solve. For example you can use different forms of representation to begin to make sense of a problem, you can use different forms to keep track of your thinking or to record results and you can use different representations to present you findings (breadth).
Skills themselves can appear in multiple guises too. For example, there are different ways in which you might break a problem down: by starting with simple cases or dividing the problem up into manageable pieces and so on (depth).
Then of course you want to have experience of solving problems in different mathematical contexts. For example, geometrical problems, statistical problems, number problems and so on. These can have quite different feels and require quite different techniques to be developed (diversity).

So some time needs to be spent on a wide range of problems to ensure learners are given the opportunity to experience, and practise, the depth, breadth and diversity of process skills and in doing so they will become more competent problem solvers.

More detailed information on problem solving and mathematical thinking skills can be found in the research section of the NRICH website - articles including " Developing a framework for mathematical thinking" and " Mathematics Enrichment: what is it and who is it for?".

You might think of all I have said so far as sitting within the mathematics. However, much of what makes an effective mathematical problem solver goes beyond mathematical practice and into developing more general attitudes and ways of thinking that encourage confidence. These more generic skills will have value well beyond mathematics but are crucial in the development of effective mathematicians.

This is the area of progression that builds upwards from the content and process elements of the curriculum. In other words, we have a third dimension:

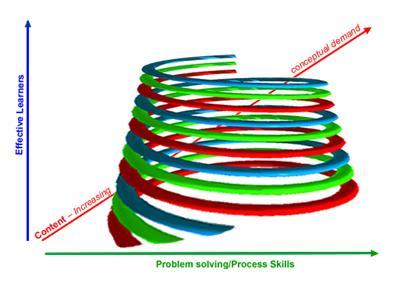
On confidence and effective learners

Effective learners develop through encouraging greater independence, reflection, resilience, participation and creativity, whilst offering contexts which are set in more complex and less familiar settings. As learners become more effective mathematicians, they also become more confident mathematicians and therefore better problem solvers. The strands of independence, reflection, resilience, participation, creativity, complexity and familiarity are ways of describing aspects of a more effective and confident mathematician. I cannot say whether confidence results in development along these strands or the development results in greater confidence. What is important is that confidence is seen as underpinning (or overarching) these ideas and is an important characteristic of an effective learner.

Explanations of the terms I have used can be found in the teachers' notes.

So let's try to see what this would look like in practice:

So, how does this link to NRICH problems?

Well, NRICH is full of resources which offer opportunities to practise and develop problem-solving (process) skills. The activities give scope for learners to work at a range of levels within those skills whilst encouraging them to move on in their thinking and confidence (the third dimension).

Using the problem Tricky Track I have tried to describe a progression in learner behaviour that might indicate development in the "third-dimension". In reality learners might vary considerably in each of the threads of development. For example, they may be very creative but not very resilient, or work independently - but only in very familiar settings or certain areas of mathematics. It is also the case that learners may score very highly in this dimension but be working at a low content-knowledge level. In other words, very young mathematicians will be very mathematical whilst working within content knowledge in line with their age.

Tricky Track

The following table gives examples of what might distinguish learners working at a low level in the "third-dimension" and those working at higher levels on the problem Tricky Track. This can inform us of learners' progression, the level at which they are working and their potential for moving on. The table also indicates some of the implications for teacher action that can influence learner behaviour.

Independence

Learners play the game and give a short answer to the problem, such as "Because it is more likely to be [this number]". They need prompting to extend their thinking and need structure for exploring their reasoning. For example, the teacher leads with suggesting pooling results to confirm suspicions. Little input on what to do is offered by the learners.	After playing the game learners need prompting to think of what to do next. However, working collaboratively, and with support, they are able to refine their ideas and come up with some proposals for moving forward and extending the problem.	Once the learners are given the starting point, they explore without further support. They extend the initial problem by asking questions of their own. They might ask for focussed advice.
The task has to be structured by the teacher. For example, the teacher suggests listing all possibilities, even leading on ways of representing the data.	The teacher uses learners' ideas to structure what happens. For example, prompting from the teacher helps learners to use their own ideas but learners do not initiate moving forward without help and the need for guidance.	Teacher acts as adviser, listening and prompting as needed.

Reflection

Learners collect results and in presenting them they tend not to consider whether there would be better ways of showing what they have found. They might compare their results with those of others but are unlikely to question what is the same or what is different and why.	Learners compare results and begin to consider what they tell them about the question. They might make some conjectures but will tend not to use what they have done to help them work on testing their ideas. Learners tend to reflect on what they have done rather than what they could do.	They make conjectures without prompting and begin to investigate them. For example, "If I played this more often would I learn any more?"; "What if the dice were not numbered 1-6?". In reflecting on what they do they come up with new ideas or questions to ask.
Teacher initiates reflection by asking key questions. For example, they share different representations and sets of results to encourage a discussion.	Teacher encourages reflection beyond methods used and the results to considering more effective or efficient methods and what other questions could be asked.	Teachers discuss ideas and share reflections with others. They encourage revision in the light of learners' reflection.

Resilience

Learners lose interest after solving (with support) the initial problem. They show no, or limited, interest in extending ideas beyond the original setting. They find it difficult to focus on discussions of the problem or on what others have to say about it. When stuck they will lose focus and give limited attention to other approaches.	Learners will extend their thinking beyond the initial problem when they have some support. They might consider one or two other ideas and begin to work on them. Returning to the problem after a break is received with some apathy! When stuck they tend to give up or perhaps try another approach, possibly because they have seen someone else using it.	Learners work on the problem for an extended period and/or return to the problem and extensions over several sessions with little prompting to continue their investigation. When they get stuck they will try to bring other ideas to bear or take an alternative route. They will discuss where they are stuck with others to see if they can help, sometimes the teacher but often their peers.
Most activity is prompted by the teacher, who manages short bursts of activity, interspersed with comment and the pooling of ideas.	Teachers draw learners back towards the mathematics by posing problems of their own and by encouraging whole group discussion of ideas and progress.	Teachers use extended tasks and "pot-boilers" as part of their everyday repertoire. For example, they will ask learners to work on extensions to the problem over several lessons.

Participation

Learners' talk is generally in response to teacher questioning and directed at the teacher. Peer to peer discussion tends to reflect what has been directed by the teacher. Learners see themselves as, and work as, individuals.	Class and group discussion is led by the teacher. Learners listen to others' explanations but do not engage at a level which enables them to question what is being said. Learners will adapt what they say and respond to the needs of different audiences when prompted. Learners begin to use others' knowledge and share ideas, mostly with prompting.	Learners offer ideas independently and take an active part in discussions, for example about the freedoms and constraints of the problem or the limitations of experimental data. They question each other and they share their ideas and listen to others, adapting their explanations to meet the needs of other learners. Learners work effectively on their own, in small groups and as part of the whole class. Learners see the value of and utilise working with others, in terms of generating and sharing ideas.
Teachers ask questions and direct discussion. They give limited time for learner response to other learners' ideas.	Teachers encourage learners to talk to each other and respond to each others' ideas. They ask for, and encourage opinions in a structured setting. For example "Xxx can you explain to us what you explored and what you found out?"; "Can anyone suggest what Xxxx might do next?".	Teachers act as guardians of the community encouraging discussion and listening rather than talking themselves.

Creativity

Learners find it difficult to make connections between mathematics, even recent mathematical experiences and the current task. Learners accept what they are told with limited questioning. Learners work on the assumption that mathematics is a series of operations which are imitated and learned by rote.	Learners may suggest ideas with prompting, for example by the teacher setting up groups and asking them to list "what the group notices". Learners begin to value and bring ideas of their own to bear on the problem. They will try something new with limited prompting.	Learners come up with their own ideas about how to test what is happening and how they can change the situation to test other ideas. They assess the merits of the ideas of others. They make connections which enable them to use prior knowledge. Learners have a number of ideas and identify ones to pursue, trying others if they reach dead ends. They control variation.
Teacher initiates and/or prompts for ideas for moving forward. "Has anyone thought about...".	Teachers ask probing questions in order to encourage learners to make connections with other mathematics. For example "Have you seen something like this before/recently?"; "Do you remember...?"; "Can you think of...?"..	Teachers respond positively to ideas and novel approaches and will encourage reflection on approaches. They will discuss freedoms and constraints with the learners.

Complexity

Learners need help in seeing the mathematics in the game. They need prompting to represent the mathematics and then utilise this to analyse the limitations of the game. Again they will need prompting to see potential variation and to decide on how to control any variation.	Learners identify the mathematics in the problem with prompting. They need help with identifying and controlling variation but can utilise their existing mathematical knowledge to begin to analyse the situation, often with limited prompting. The group begin to play the game and can identify features of the game (such as its relative fairness).	Learners see the mathematics in the problem and begin to analyse it in terms of the mathematics they see. They identify, utilise and control variables, such as number of, and numbers on the, dice. They represent information and findings in different ways that are influenced by perceived need. For example they might use tables and tallying to collect the data and bar charts to show results and be able to justify their choices. Learners make connections between the game and other mathematical experiences and knowledge. They ask questions of their own and identify ways of trying to answer them.
The mathematics in the game, possible questions to answer and how to work on testing ideas is prompted by the teacher.	The teacher offers support in helping learners to make mathematical sense of what they see and experience.	Teachers work with learners as mentors asking key questions and challenging their use of variables. They press for clarity and precision.

Familiarity

Learners play the game and make limited connection with other games they have played before. They need guidance in identifying the mathematics and therefore starting on analysing the problem. They find ways of representing data in an organised way after prompting.	Learners are able to make sufficient sense of the situation, using prior knowledge of similar settings, to enable them to record findings and draw conclusions independently. They do not overtly make connections with the other similar situations, or bring knowledge developed in those situations, to bear in developing questions of their own.	Learners are able to identify the mathematics in the game and relate it to other games or contexts they know (for example the Lottery). They use their knowledge of similar settings to help them to identify a starting point and to pose questions of their own.
The teacher gives space for exploration and uses the ideas of learners to encourage more organised recording and analysis. They make connections with similar experiences and discuss the value of different approaches.	The teacher will encourage comparison of methods and relate activity to other similar experiences of which they are aware. For example, getting a double six to start a game or the best properties to buy in the game of Monopoly.	The teacher draws on learners' knowledge to talk about the connections, similarities and differences between the situation, and the related mathematics, and other situations the learners identify.

Conclusion

Assessing Pupil Progress is about supporting learning. Its aim is to help teachers to find out more about their pupils' strengths and weaknesses, and help them plan for learning that takes into account learners' individual needs. Whilst there is a need to keep track of what a pupil can do and where they might go next, APP is not about ticking hundreds of boxes, levelling every piece of work, or doing additional assessment activities in addition to those you already undertake at school. It is about knowing what might come next on a learner's journey and offering opportunities for that learner to progress.

Pedagogy. Learning mathematics. Rich Tasks. Mathematical modelling. Mathematical Thinking. Group worthy. Real world. Problem solving. Enrichment. Assessment.