Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Fencing



You might like to look at Fencing in Lambs before looking at this challenge.
What we're about this time is using some fences that will give a good rectangular space to keep things in. The fences are quite thick and stand up on their own. You might like to use some Multilink cubes or other cuboids and pretend that they're the fences. Ask your teacher at school and they will be able to find some blocks to help.
Suppose we start off with four of these fences and put them together like this:-
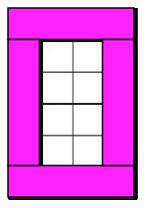
The space I've made is $8$ squares [centimetres in my case].
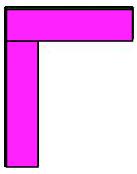
Notice that the corners are good strong corners like this one:-
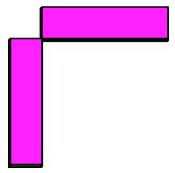
We do need strong corners and not weak ones like :-
The next one I could do uses five fence panels instead of four. So I get:-
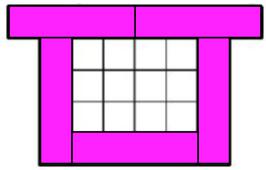
Now my space is bigger - it is now $12$!
I know I've wasted a bit of two of the fences but it was the only way I could think of using five!
Using six is much easier:-
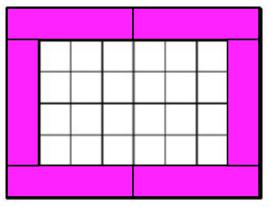
And using seven turns out like this when I try it:-
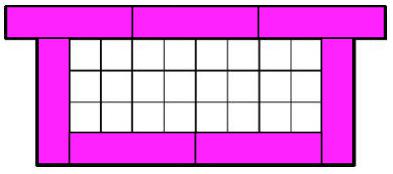
The area of the space has now increased to $24$!
My challenge starts off with asking you to have a go with blocks that are a bit like mine [$4$ long and $1$ wide].
Do you know you could possibly even try using some house building bricks as some of these are about four times as long as wide! BUT I'M PARTICULARLY ASKING YOU TO ARRANGE YOUR FENCES SO AS TO MAKE THE SPACE THE LARGEST RECTANGULAR SPACE IT CAN BE, first with FOUR, then FIVE, then SIX etc.
REMEMBER ABOUT THE STRONG CORNERS!
By the way, the way I've arranged my fences has not always given the largest rectangular space inside.
Now I guess you might like to find a good way of recording what you managed to do.Now my question "I wonder what would happen if ...?" just has to be: "I WONDER WHAT WOULD HAPPEN IF THE FENCES WERE $5$ LONG INSTEAD OF $4$?"
Well I'll start you off on this challenge
REMEMBER ABOUT THE STRONG CORNERS!
Here's the first few ... but not necessarily ones that give the biggest space, that's for you to discover.

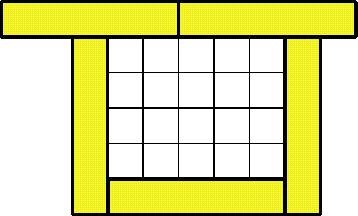
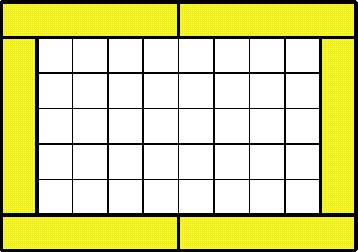

Now you try to sort your own out!
When you think about how you can put your results down, it may be good to link them with the ones when the fences were $4$ long.
Now of course you can go to lengths of $6$, $7$, $8$, $9$ etc. etc.
What a lot to explore!
How about looking at your results and seeing what patterns you notice and what predictions you can make?
Photographs of your fence models would be good to have to put with the solutions.

