Euler's buckling formula
Problem
When you apply a steadily increasing axial load to an initially-straight strut after a while it will start to bend, and then, when a critical load $P$ is reached, it will buckle. You could try it with a matchstick.
Euler showed that at the point of buckling the strut is in a static equilibrium state: like a ball balanced at the top of a slope where the slightest push will cause it to roll down. At each point along the beam the moment due to the bending stiffness and the moment due to the axial force being applied are perfectly in balance, and if you increase the load by just a tiny bit it will break.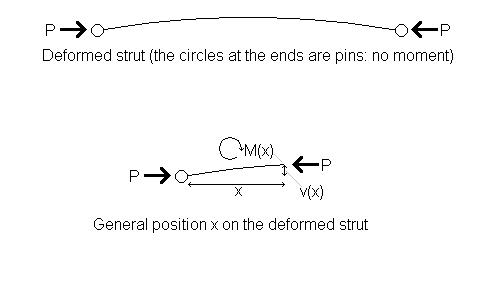
By considering a general position $x$ on the deformed strut, you can derive Euler's basic formula for $P$ by constructing and solving a second order differential equation.
You need to know two new engineering formulae: The moment due to stiffness is $M = B \kappa$, where $B$ is bending stiffness (a property of the beam) and $\kappa$ is curvature. You also need to know that we can approximate $\kappa$ as $-\frac{d^2v}{dx^2}$, where $v$ is displacement in the direction perpendicular to the initial direction of the beam (see Beam Me Up for a derivation of this).
Getting Started
In the second diagram, at the point $x$ what is the moment due to the axial force?
The mathematics behind moments of forces are typically covered in early A-level Mechanics modules. The methods for solving 2nd order differential equations are typically done in the A-level module FP2.
Student Solutions
Equating the applied moment to the moment in the beam
$Pv(x) = M(x) = B\kappa(x) = -B\frac{d^2v}{dx^2} = -Bv''$
$\therefore Bv'' + Pv = 0$
Thus we wish to solve $v'' + \frac{P}{B}v = 0$.
$m^2 + \frac{P}{B} = 0$ is the 'subsidiary equation', $\therefore m = \pm i\sqrt{\frac{P}{B}}$.
$\therefore v = G\sin(\sqrt{\frac{P}{B}}x) + H\cos(\sqrt{\frac{P}{B}}x)$ where $G$ and $H$ are constants.
But $v(0) = 0 \therefore H = 0$
and $v(L) = 0 \therefore L\sqrt{\frac{P}{B}} = n\pi$, where $n$ is any integer.
$\therefore P = \frac{B n^2\pi^2}{L^2}$, and since the lowest possible $n$ is 1, and we are interested in the lowest load that would be an 'equilibrium state' when the strut is on the point of buckling, we find the lowest buckling load is given by
$P = \frac{\pi^2B}{L^2}$
So now you can find out just how stiff that matchstick is! Later you will learn that the bending stiffness $B$ is the product of two other quantities, the 'elastic modulus' material stiffness $E$, and the lowest 'second moment of area' of the beam $I_{xx}$.
