1. In the beginning ...
Knowledge about the possible beginnings of human mental development comes from research on the co-evolution of language and the human brain. The central idea that comes out of this research is that mankind, uniquely, is what is called a 'symbolic species'. That is, we have the ability to make ideas 'visible in the mind'. This means we can create, manage, manipulate and blend images in ways
that help us to form new relationships and produce new concepts.
We can only speculate on the earliest stages in the development of mathematics but we do have evidence which shows that we have the power to visualise and represent physical objects in our mind. This power is seen in the representations of counting, bartering and building activities of early civilisations. In particular, our perceptions of symmetry seem to have produced many kinds of geometrical
representations in different cultures.
2. The Pythagoreans (c. 550 - c. 450 BCE)
Imagine, for example, what might be done with arrangements of stones in the sand:
In these images, a square pattern has been divided into different areas, making rectangles or triangles.
In the above two images, other shapes have been produced, leading to speculations about relationships between numbers and areas, and it is thought that the elementary number theories of the Pythagoreans might have been generated by images like these [see Note 1 below].
Further manipulation, dissection of squares and rearrangement, leads to images of right-angled triangles and the familiar relationship between numbers and areas. For example:
3. Egypt: The Rhind Papyrus.
Early methods for solving problems come from the Rhind Mathematical Papyrus, written in Egypt about 1,550 years BCE. It is a 'problem text' of exercises for training scribes, who were the administrators. It has examples of methods for weighing, measuring and surveying, for finding areas and volumes, and for working out rates of pay for workers of various kinds.
|
|
In particular, the Papyrus has a series of problems showing how to solve what we could call 'linear equations' by a method that became commonly used by merchants throughout the Mediterranean countries for some three thousand years, called the 'Method of False Position'. It is used for all kinds of calculations involving comparison of values and quantities. This
method still appeared in school text books in the early 20th century. |
Here is Problem 26:
This belongs to the group of '$h$' problems, sometimes written as 'heap' meaning 'quantity' or 'number'. $\bar{4}$ is an example of the usual way we represent Egyptian 'unit' fractions.
| In a quantity and its $\bar{4}$ (is added) to it so that $15$ results |
|
A quantity is added to a quarter of itself and the answer is $15$
|
|
Calculate with $4$
You shall calculate its $\bar{4}$ as $1$. Total $5$.
|
|
You begin by assuming $h = 4$,
so, as the left hand side is $h + \frac{h}{4}$
this gives $4 + 1=5$:
$h = 4$ does not work as it gives an answer of $5$ not $15$.
|
Work with $5$ to find $15$.
\ . $ ~~~~~5$
\ $2~~~~10$
$3$ shall result.
|
|
Now take the $5$ and divide it into $15$ to get $3$. |
|
Multiply $3$ times $4$
$~.~~~~~~3$
$~2~~~~~6$
\ $4~~~~12$
$12$ shall result
|
|
Multiply the $4$ by $3$ to find the result you want, $12$. |
|
. $~~~~12$
$\bar{4}~~~~~ 3$ total $15$
The quantity $12$ its $\bar{4}~~~3$.
Total $15$
|
|
So, $12$ add a quarter of $12$ is $15$. |
In modern notation, the problem looks very easy: $$h + \frac{h}{4}=15$$
We begin by using $h=4$ which immediately makes the fraction $\frac{h}{4} = 1$
So the left hand side is $5$, but we need $15$.
If by using $4$ we obtain $5$, what do we need to use to get $15$?
|
|
The sundial was one of the first instruments used for measuring time, and the properties of the right-angled triangle were well known to ancient people (Problem 56 deals with similar triangles). The slopes of pyramids and other sloping surfaces were measured by the 'seked' - the horizontal distance measured for every cubit of height. |
Visualising a triangle like this would make the problem much simpler and the ratios could then easily be compared. $$\frac{\mbox{'}h\mbox{'}}{15}=\frac{4}{5}$$
So, for the denominator of the right hand ratio to be $15$, we need to multiply the numerator and denominator of the ratio $\frac{4}{5}$ by $3$.
4. Early Indian Mathematics (c. 1500 - 500 BCE)
Similar traces of the above kind of visualisation appeared in the Indus valley in roughly the same period, although there are claims that the procedures were much older [see Note 2 below].
The Vedic people entered India about 1500 BCE. The name comes from their sacred rituals called the Vedas. These date from about the 15th to the 5th century BCE and were used for sacrificial rites which took place at an altar.
The name Sulbasutras (meaning 'cord-rules') applies to the part of the Vedas which gives the rules for building the brick altars used in ritual sacrifice. Instructions were given:
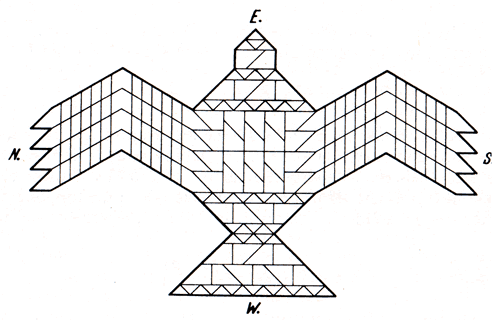
"He who desires heaven is to construct a fire-altar in the form of a falcon" and "a fire-altar in the form of a tortoise is to be constructed by one desiring to win the world of Brahmin" [see Note 3 below]. Many of these instructions contain transformations for preserving areas, such as changing a rectangle into a square of the same size. See examples below:
|
|
For two squares of the same size, it is easy to see how to combine the areas to make one square, but not obvious for squares of different sizes.
|
"If it is desired to combine two squares of different measures, a [rectangular] part is cut off from the larger [square] with the side of the smaller; the diagonal of the cut-off [rectangular] part is the side of the combined square."
"Alternatively if it is desired to combine two squares of different measures, a rectangle is formed with the side of the smaller [square] [as breadth] and that of the larger [as length]; the diagonal of the rectangle [thus formed] is the side of the combined square."
These instructions clearly show a knowledge of the 'Pythagorean relation'.
The base line for the altar was always East - West and careful and precise interpretation of the instructions enabled the priests to build the falcon 'fire-altar'.
The Sulbasutras were written in Sanscrit and the texts often used 'code words' or abbreviations for lengths, areas and other quantities. For example, the word 'eyes' represented number two and 'teeth' represented 'thirty-two', so a sentence might read something like: 'we have the eyes, so do this to find the teeth', and the geometry was hidden under a cloak of instructions coded in number
language.
5. Old Babylonian Mathematics (c. 1850 - 1600 BCE)
The earliest mathematics appeared in Mesopotamia some 3,500 or more years BCE with a variety of specific number systems for trading with different things like grain and cereals, milk and dairy produce, or things made out of clay or wood. The 'sexagesimal system' as it is popularly known, appeared before 2000 BCE and was well-established by the time of Hammurabi, (1795-1750 BCE) the first
king of Babylon. Most of the well-known evidence we have on clay tablets comes from the Babylonian Kingdom period that ended about 1600 BCE.
Accounts for cereals, beer or oil - about 3,000 BCE
The 'Old Babylonian' Empire had a well-organised society with an efficient administration which enabled scribes to administer social justice through a system of fair management and distribution of goods. Central to this system were the schools where scribes were trained. The school culture was basically oral, depending on the memorisation of texts and routines for
calculation; tables for multiplication, division, reciprocals and other useful units were available. Emphasis on administration, labour management and quantity surveying led to the use of 'word problems' that could be solved using standard algorithms such as:
'Cut and Paste' Geometry: Removing a Square from a larger Square.
The claim that the Babylonians were doing 'arithmetical algebra' (or even quadratic equations) is now seen as an error. Recent research into the language has tried to recover the original thought processes, and shows that the underlying concepts were essentially geometrical. We don't really need the algebraic labels here, because the geometrical procedure is quite general. The size of the
smaller red square does not matter, and the numerical instructions hid the underlying geometrical visualisation [see Note 5 below].
Word Problems
This example of a 'sum and product' problem is from a Babylonian 'school tablet'. The problem has been rewritten to convey the geometrical nature of the original procedure [see Note 6 below].
|
Length, Width.
I have raised, length and width. Surface: $252$
I have put together length and width: $32$
$32$ put together,
$252$ surface: $18$ length, $14$ width
|
|
The problem and answers are stated,
and the method is described.
|
| This is the way of doing it: |
|
Here is the arithmetic: |
| $~~~~~$break off half of $32$: this gives $16 $ |
|
$\frac{32}{2}=16$ |
| $~~~~~$raise $16$ by itself: $256$ |
|
$16^2=256$ |
| $~~~~~$leave out the surface: $256 - 252 = 4 $ |
|
$256-252=4$ |
| $~~~~~$find the side of this square $4$: it is $2$ |
|
$\sqrt{4}=2$ |
| $~~~~~$put together $16$ and $2$: $18$ length |
|
$16+2=18$ |
| $~~~~~$tear out $2$ from $16$: $14$ width |
|
$16 - 2=14 $ |
| I have raised length and width. $~~~~~ 252 $ |
|
$(16+2)(16-2)=252 $ |
The visual thinking behind the calculation appears to have gone like this:
We have the area of a rectangle, $252$;
We have the sum of its length and width, $ 32$ (the semi-perimeter);
We know from practical experience (see diagram above); that by removing a small (red) square from a larger (blue) square, we can make a rectangle.
So, if we make the side of the large square half of $32$; then the area of the large square will be $256$.
Now take away the rectangle, (area $252$), and we are left with the small (red) square.
Geometrically, this will always work whatever the lengths of the sides concerned. Arithmetically , the problems were arranged so that the numbers used in the calculation always resulted in a perfect (red) square.
Many more examples like this have been discovered, and as well as the underlying geometrical visualisation, there is also the clear emergence of an algorithmic process . The Babylonians had established one of the important essential aspects of problem-solving. They had established a method for solving particular types of
area problems , and it was this method that was taken over by later generations of scholars and eventually developed into the algorithm we use in classrooms today.
6. Greek Geometry
By about 350 BCE the numerical and intuitive geometry of these cultures was changed into the deductive science we know as Euclidean Geometry. Book II of the Elements, (still often labelled 'geometric algebra') contains much of the knowledge discussed above in terms of geometric theorems. The transformation of rectangles and parallelograms into other shapes of equal area is demonstrated in
general terms from a deductive point of view. The myth that the Greeks could not deal with irrational magnitudes has no basis in fact. The first diagram below shows how, from rational measurements of the sides of the rectangle, it is possible to create a square with non-rational sides [see Note 7 below].
Constructing a square equivalent in area to a rectangle
|
|
|
The red side of the rectangle is brought into line with the upper blue edge by drawing an arc (radius r ). The (red + blue ) line is bisected to find the centre of a circle, and a semi-circle is drawn. The side of the square required is the green vertical line. |
| |
|
|
|
|
|
In this diagram there are three similar right-angled triangles, APB in the semicircle, AXP and PXB. The coloured sides of the triangles correspond to the diagram above. The relationship shown is the equivalence of corresponding ratios. |
Thomas Heath, in his translation of Euclid [see Note 8 below], states:
"For want of the necessary notation the Greeks had no algebra in our sense. They were obliged to use geometry as a substitute for algebraical operations; and the result is that a large part of their geometry may appropriately be called 'geometrical algebra'."
So for Heath, referring to the diagram above, and in modern notation,$$ \mbox{ if } AX = a, ~XB = b ~\mbox{and} ~PX = x,~ \mbox{then}~ ab = x^2$$
This attitude influenced the way we interpreted much of Greek mathematics as algebra until quite recently.
7. The Arab Civilisation
The Abbasid Caliph al-Mansur (754-755) moved his capital to Baghdad in 762 CE. Euclid was translated into Arabic by al-Hajjaj later in this century, and Indian scholars brought Brahmagupta's astronomical works where they were translated into Arabic. The work of Diophantus was also translated and Baghdad became a centre for learning, attracting many scholars from the known world. Later, the
Caliph al-Ma'mun (813-833) established the 'House of Wisdom', which through the 9th and 10th centuries acted as a centre for the great translation programme of knowledge that scholars had accumulated and had built on through their own discoveries.
Out of this accumulation of knowledge came solutions to problems asking for the discovery of numerical and geometrical unknowns, and Islamic civilisation created and named a new science - Algebra.
Conceptual Blending
The scholar al-Khowarizmi (c770-c840 CE) took advantage of the works that had been translated and wrote Al-Kitab al-mukhtasar fi Hisab al-gabr wa'l-muqabala , (The Compendious Book on Calculation by Completion and Balancing) and from this title we take the word
'Algebra' from 'al-jabr', meaning 'setting back in its place', or 'restoring'. Al--Khowarizmi's name also gives us the words 'algorithm' or 'algorism'.
Portrait of Al-Khowarizmi $~~~~~~$ A page from the Algebra
Al-Khowarizmi was probably first among a number of scholars who showed how the geometrical constructions of Euclid Book II and the arithmetical heritage from Diophantus' Arithmetica , and the ideas from the Middle East and Indian scholars could be shown to be equivalent. What is special about Al-Khowarismi's conceptual blending is that for the first
time we find the objects of study (the unknowns) and the equations that define clearly the classes of problems to be solved.
|
The six cases of equations were:
- Roots equal numbers
- Mal [see Note 9 below] equal roots
- Mal equal numbers
- Mal and numbers equal roots
- Mal and roots equal numbers
- Mal equals numbers and roots
|
|
In our notation:
- $px = q$
- $x^{2} = px$
- $x^2 = q$
- $x^2 + q = px$
- $x^2 + px = q$
- $x^2 = q + px$
|
Case 5. Square and Roots are Equal to Numbers
One square and ten roots of the same, amount to thirty-nine dirhams [see Note 10 below].
"This means, what must be the square which, when increased by ten of its own roots, amounts to thirty-nine?
The solution is this:
You halve the number of roots, which in this case gives five.
This you multiply by itself, the product is twenty-five.
Add this to thirty-nine, the sum is sixty-four.
Now take the root of this, which is eight, and subtract from it half the number of roots, which is five, the remainder is three.
This is the root of the square you sought for, and the square itself is nine.
The solution is the same when two squares or three, or more or less are specified. You reduce them to one single square, and in the same proportion you reduce the roots and simple numbers which are contained therewith."
Notice that the words of the procedure indicate almost exactly the same actions as in the Babylonian Algorithm.
Although the Arabs were probably aware of negative numbers at this time, because they had translated Brahmagupta's work, (Reference:
History of Negative Numbers ) the equations were arranged so that the numbers were all positive. Clearly, if the visualisation of the geometric model involves squares and rectangles,
these areas must be represented by positive quantities.
Case 4. Squares and Numbers are Equal to Roots.
Example :
A square and twenty-one in numbers are equal to ten roots of the same square.
"That is to say, what must be the amount of a square, which when twenty-one dihrams are added to it, becomes equal to the equivalent of ten roots of that square?
Solution:
Halve the number of the roots, the half is five.
Multiply this by itself, the product is twenty-five.
Subtract from this [my italics] the twenty-one which are connected with the square;
the remainder is four.
Extract its root, it is two.
Subtract this from the half of the roots, which is five, the remainder is three. This is the root of the square which you required, and the square is nine.
Or, you may add the root to the half of the roots, the sum is seven.
This is the root of the square which you sought for, and the square is forty-nine."
|
|
|
Compared with the Babylonian word problem in section 5 above, this is another case where the semi-perimeter of the sides of the rectangle are given, so that the area of the square made with half the root is larger than the area of the rectangle. In this case the algebra of his first solution is:$$\frac{10}{2}-\sqrt{\frac{10^2}{4}-21}$$
and his second procedure is $$5+\sqrt{5^2-21}=7$$ which gives the diagram opposite, where the $7 \times 7 = 49$ fills the empty space.
|
"When you meet with an instance which refers you to this case, try its solution by addition, and if that does not serve, then subtraction certainly will.
For in this case, both addition and subtraction may be employed, which will not answer in any of the other three cases in which the number of roots must be halved. And know that when in a question belonging to this case you have halved the number of roots and multiplied the half by itself, if the product be less than the number of dihrams
connected with the square, then the instance is impossible, but if the product be equal to the dihrams by themselves, than the root of the square is equal to the half of the roots alone, without either addition or subtraction."
So, in terms of our algebra, and referring to our usual quadratic formula, he recognised that when '$b^2 + 4ac$' is positive there are two possible solutions, and when he says ", if the product be less than the number of dihrams connected with the square, then the instance is impossible" he has recognised that'$b^2 + 4ac$' is negative, and when '$b^2
= 4ac$' he says there is only one root.
After the breakthrough by al-Khowarizmi, other Islamic scholars tried to show that that geometrical demonstrations of the solutions of these problems were possible. The most successful of these was Thabit ibn Qurra (836 - 901 CE) who finally provided general Euclidean proofs for all the six cases by comparing them to the theorems in Euclid Book
II.
It was some time before all this knowledge was passed on to European scholars, but the formulas and routines for solving these problems persisted in the texts used by the merchants, but the geometrical background began to disappear from view. When the Greek and Arabic knowledge began to be translated into Latin, European scholars at last discovered the secrets of what came to be called 'The
Cossic Art'.
N.B. Pedagogical notes related to the history of algebra discussed here can be found by clicking on the " Notes' tab at the top of this article .
Notes
-
Evidence for this kind of activity is deduced from fragments of writings by the early Pythagoreans. Also, the elementary number theory in Euclid Book VII. Katz (1998) has a section on the Pythagoreans (pp. 48-51)
-
The dating of early Indian mathematics has always been controversial. As with other civilisations it was basically an oral culture, and what was written down appeared long after it was first conceived. Added to this the Indian scholars wrote on palm leaves that rotted away quite quickly in the humid climate. Documents were copied and copied many times, so we never have the original text and it
is virtually impossible to reconstruct the early history of Indian mathematics with any certainty.
-
Quoted from Kim Plofker's chapter on Indian Mathematics in Katz (2007 p.387).
-
Both quotations are from the Baudhayana - Sulbasutra (c. 1,000 - 500 BCE) in Kim Plofker's chapter 4 in Katz 2007.
-
Evidence for this geometrical basis comes from recent research into the language and culture of the period by a group including Jens Hoyrup from Roskilde University in Denmark and Eleanor Robson from Cambridge.
-
This is my version of the problem using Hoyrup's (1984) Babylonian 'word list'. See also Pedagogical Notes item 5.
-
The 'Pythagorean' diagram on the right hand grid in section 1 above has a rational area of 5 units, and non-rational sides.
-
Heath, T. L. (1963) A Manual of Greek Mathematics. Dover (original Oxford University Press, 1931)
-
'Mal' was Euclid's word for 'wealth' (the unknown).
-
A Dihram is a unit of currency, still used in the Arab Emirates.
-
All translations in this section are quoted from Berggren, Chapter 5 in Katz (2007).
References
This list indicates the main sources I have used in this story. For the school or college library, I suggest Katz (2007) and Robson & Stedall (2009) as the best available sources for the new research and attitudes to mathematics of the ancient world.
Berggren, J.L. (1986) Episodes in the Mathematics of Medieval Islam. New York. Springer.
This book shows how the Islamic scholars developed the arithmetic, geometry, and trigonometry they translated from different sources, and how this knowledge helped them develop the new science of Algebra.
Hoyrup, J. (1985) Babylonian Algebra from the Viewpoint of Geometrical Heuristics. Roskilde University Centre, Roskilde, Denmark.
This is the seminal work that helped to develop new ways of looking at the mathematics of the past. It examines the language and culture of ancient Iraq and provides new translations of much of the available material.
Katz, Victor, J. (1999) (Second Edition, Corrected) A History of Mathematics: An Introduction. Harlow, England. Addison-Wesley.
The best, most comprehensive and up-to-date general history of mathematics available.
Katz, V. (2007) The Mathematics of Egypt, Mesopotamia, China, India and Islam. New Jersey. Princeton University Press.
Four internationally renowned authors write on their own subjects of expertise. This is the real background for the 'elementary' mathematics taught in school: Arithmetic, practical geometry, proto-algebra and trigonometry.
Plofker, Kim (2009) Mathematics in India. New Jersey. Princeton University Press.
This is a comprehensive and expert treatment of the history of Indian mathematics.
Robson, Eleanor. (2008) Mathematics in Ancient Iraq: A Social History. New Jersey. Princeton University Press.
This book sets mathematics in the social, cultural and economic context of ancient Iraq; it shows how an oral, visual culture developed the practices of sophisticated mathematics in response to economic and political influences.
Robson, Eleanor & Stedall, Jackie (2009) The Oxford Handbook of the History of Mathematics. Oxford. Oxford University Press
This history of mathematics is quite unlike any other. It draws on a wide variety of experts who show how mathematics was developed and used in different cultural contexts and the diversity of what we call mathematical practice.
If you can reach a library that carries journals in mathematics education, then you might find the following article of interest:
Arcavi, A. (2003) The role of visualisation in the learning and teaching of mathematics. Educational Studies in Mathematics 52 (3) 2003 (215-224)
Weblinks
This is the most comprehensive easily navigable website for the History of Mathematics.
http://www-history.mcs.st-and.ac.uk/history/
http://nrich.maths.org/public/viewer.php?obj_id=6001
http://nrich.maths.org/public/viewer.php?obj_id=5747