Griddy Region
What is the area of the region common to this triangle and square?
Problem
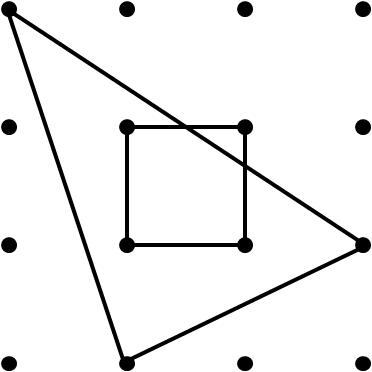
The dots are one unit apart. What is the area of the region common to both the triangle and the square (in square units)?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
$$\frac{11}{12} \; \text{square units}$$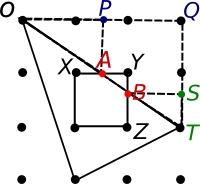
We want to find out how far the points $A$ and $B$ (the points on both the triangle and square) are from $Y$. The triangle $OQT$ is $3$ units across by $2$ units down. The triangle $OPA$ is similar to $OQT$, and is half its size (since it is one unit down rather than two). So the point $A$ is $\frac{3}{2}$ units from $O$, so $\frac{3}{2}-1=\frac{1}{2}$ unit from $X$, so
$1-\frac{1}{2}=\frac{1}{2}$ unit from $Y$
Similarly, the triangle $BST$ is $\frac{1}{3}$ the size of $OQT$, so the point $B$ is $\frac{2}{3}$ unit from $Z$, so $1-\frac{2}{3}=\frac{1}{3}$ unit from $Y$. So the triangle $AYB$ has area $$\frac{1}{2}\times \frac{1}{2}\times \frac{1}{3} \; \text{square units}= \frac{1}{12}\; \text{square units}$$ so the area of the overlap is $$1-\frac{1}{12}\; \text{square units}=\frac{11}{12}\;
\text{square units}$$
