Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Lengthy Journeys
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Lengthy Journeys
Here is a simple map showing the positions of 5 cities:

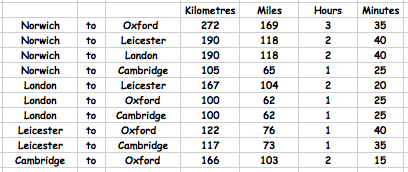
These numbers show us direct routes. But now, suppose we go on journeys involving three or four cities.
For example, we could go from Norwich to Oxford but go through Cambridge on the way.
Or, we could go from London to Leicester but go through Oxford on the way.
What other journeys involving three or four cities can you find?
When you have some of these answer these questions:
1. What is the total distance of your journey in kilometres?
2. How many minutes long is your journey?
3. How much longer (in terms of time) is the journey when passing through another city or other cities along the way compared with the direct journey between the starting city and the final destination?
Now you could try and find the longest route (in terms of distance) for visiting all five cities.(We might decide that we will only visit each city once.)
What about the shortest route for visiting all five cities?
How much longer does it take to travel the longest route compared with the shortest route?
Why do this problem?
This problem may be used to introduce pupils to handling more complicated data and gives them the opportunity to calculate using distance and time.
Possible approach
It would be nice to have a map of the UK to start off this problem (or for pairs of children to have an atlas or road map) and ask pupils to locate the cities in question. You can then draw attention to the simplified map in the problem. To encourage learners to engage with the information in the table, you could ask a few starter questions, such as "how far is the journey from Oxford to
London?" and "what journeys could you make in under 3 hours?".
This problem lends itself to being tackled in groups, for example of three or four pupils. Ask each group to try to answer the questions and as they are working, look out for those groups who are communicating well and perhaps those who divide the task amongst themselves. You might like to ask groups who have organised their approach well to share their strategies with everyone else. The
main point of this activity is for children to be immersed in the data so that they begin to use it confidently.
You might like to have a whole-class discussion about the ambiguity of "long" in this context. Does it mean distance-wise or time-wise? Does it matter?
Key questions
What other journeys could you make, for example, starting at Norwich and ending at Oxford?
How are you going to keep track of which routes you have found?
What pieces of information do you think would be good to find in order to work out the total distance and total time taken?
What would you like to look at first in trying to get an answer?
Possible extension
You could encourage the pupils to create their own questions based on the information given.

