Putting two and two together
Problem
Two equilateral triangles can be put together in one way only, if they must touch all along a side:

These isosceles triangles of the same area can be put together in more than one way.
Remember that reflection can be used as well as rotation when finding the ways.

Can you find any other ways?
You could cut out triangles from these sheets.
These triangles are half of the above equilateral and isosceles triangles:

In how many ways do you think two of these can be put together using, reflection as well as rotation, if same-sized sides must touch the full length of the side?
Can you give any reasons for this?
You could cut some of your other triangles in half to test out your prediction.
Can you find a triangle such that two identical copies of it can be put together in more ways keeping to the rule that same-sized sides must touch the full length of the side?
Getting Started
You might find it helpful to have lots of triangles cut out so you can try out your ideas. You could print off these sheets, or use the interactivity to work on the green triangle part of the problem.
Remember you can only join sides that are the same length, so which sides will join to which?
Once you have joined two sides, can you join the same sides in any other ways?
How will you record the shapes you have made?
Student Solutions
Caroline from St Jude's C of E School said that she found one more way to put the green (isosceles) triangles together. She sent this picture of all three ways:

Sally says thereis one more way than this, as because we are not allowing reflection of the triangles themselves, then we could make the longer shape again, but the other way round, so the down pointing triangle was to the right of the up pointing triangle.
Caroline then goes on to suggest:
The half equilateral and isosceles triangles can be joined in three ways, because the triangles have three different length sides.Francesca noticed:
The two blue triangles are the same, just reflected of each other. They are scalene because all their angles and sides are different lengths. They are also Right Angled Triangles.
So if there are three different edge lengths, and then also two ways of rotating the other triangle to place it there are 6 ways like in my picture.
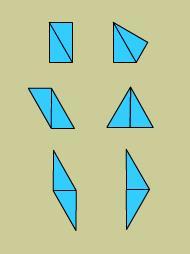
Great! Why not now explore putting the yellow, blue and green triangles all together. Watch out for different edge lengths!
If anyone has any further ideas, please do get in touch with us.
Teachers' Resources
Why do this problem?
It is essential to have cut-out triangles available for the children to manipulate while working on this problem. You can print off these sheets, if possible on coloured card.
