Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Article by Jennifer Piggott
Published 2011 Revised 2016
Meet the Nim Family
We all enjoy playing games and experience tells us that games can be very productive learning activities. However, before we commit ourselves to playing games in maths lessons, we need to answer the following questions:
- What is the justification for the use of games in mathematics lessons?
- Are some games better than others?
- What educational benefits are there to be gained from games?
This article considers the nature of games and their role in supporting pupils in thinking creatively - particularly when trying to identify winning strategies. Oldfield (1991) says that mathematical games are activities which:
- involve a challenge, usually against one or more opponents;
- are governed by a set of rules and have a clear underlying structure;
- normally have a distinct finishing point;
- have specific mathematical cognitive objectives.
To illustrate some of the points I will focus on the game of Nim its relatives. Nim-like games have been played since ancient times. They are thought to have originated in China but the earliest references to Nim in Europe were at the beginning of the sixteenth century.
Nim is a strategy game in which players capture objects. The player to take the last object wins. Nim can also be played so that the person who makes the last move (who takes the last object or reaches a particular total) loses. All the examples used here can be found on the NRICH website; several of them are interactive.
Got It
Got It is an interactive version of the classic game of Nim. It involves players taking turns in adding numbers to reach a chosen target (for example, any of the numbers 1, 2, 3 and 4 to reach a target of 23).
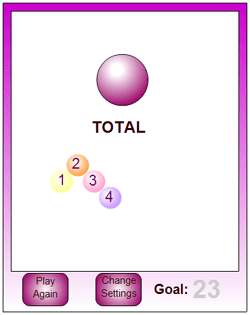
Pupils are asked to work out a winning strategy and then:
- explore whether it matters who goes first
- identify how the strategy changes if there is a different number
- consider whether changing the target number influences who should go first
- identify how the strategy changes if you have more numbers to choose from (for example, 1-6)
- find a generalisation for who would win for any target number and any group of consecutive adding numbers starting from one
What is a mathematical game?
When considering the use of games for teaching mathematics, it is useful to distinguish between an activity and a game. Gough (1999) says that:
A game needs to have two or more players, who take turns, each competing to achieve a winning situation of some kind, each able to exercise some choice about how to move at any time through the playing.
The key idea in this statement is that of choice. In this sense, something like Snakes and Ladders is NOT a game because winning relies totally on chance. The players make no decisions, nor do they have to think further than counting. There is also no interaction between players - nothing that one player does affects any other player's turn in any way.
There are many activities that we would describe as games, which can be used to test mathematical understanding or practice skills - for example, matching card games, games of odd one out and so on. There are an enormous number of such games which support work in number, algebra and geometry, and many can be found on the NRICH site itself. However, these latter types of "games for practice"
are not of the sort Gough has in mind. Got It is such a game because it requires pupils to think about a strategy, not dependent on chance, to acheive a winning position.
More noticeably, Got It also offers a context in which pupils can pose their own problems and investigate the environment created by the game. They have to work out the mathematics and consider how maths helps them win the game. Pupils will be engaging in an investigation of a particular context, but they may be able to apply their findings to other, similar games. Pupils should then be
encouraged to make their own Nim-like games based on similar strategies and, through this, consider the underpinning mathematical principles and think creatively about how to test out their conclusions. They can also pose questions such as: "Is the game fair and is there a certain strategy for winning?"
Benefits of Using Games
The advantages of using games in a mathematical programme have been summarised in an article by Davies (1995) and include:
- Meaningful situations for the application of mathematical skills are created by games
- Motivation. Children freely choose to participate and enjoy playing
- Home and school. Games provide "hands-on" interactive tasks for both school and home.
- Positive attitude. Games provide opportunities for pupils to build positive self-concepts and develop positive attitudes towards mathematics, through reducing the fear of failure and error.
- Increased learning in comparison to more formal activities. Deeper learning can occur through games due to the increased interaction between children and opportunities to test intuitive ideas and problem solving strategies.
- Different levels of thinking. Games can allow children to operate at different levels of thinking and to learn from each other. In a group of children playing a game, one child might be encountering a concept for the first time, another may be developing his/her understanding of the concept, a third consolidating previously learned concepts.
- Assessment. Children's thinking often becomes apparent through the actions and decisions they make during a game, so the teacher has the opportunity to carry out diagnosis and assessment of learning in a non-threatening situation.
- Independence. Children can work independently of the teacher. The rules of the game and the children's motivation usually keep them on task.
- Make sure the game matches your mathematical objective.
- Use games for specific purposes, not just time-fillers.
- The game should have enough of an element of chance so that it allows weaker players to feel that they have a chance of winning.
- Keep the game completion time short.
- Use five or six 'basic' game structures so the children become familiar with the rules - vary the mathematics rather than the rules.
- being systematic
- transforming information (e.g. inventing a method for recording moves)
- searching for patterns
- applying mathematics (e. g. doing calculations and algebra)
- manipulating variables
- working backwards or simplifying the problem
- hypothesising and testing
- generalising (perhaps even producing a formula)
Variations of the Same Game
This small group of activities is taken from the Mathematical Games Archive on the NRICH site. They all have a related structure that can be used to develop the skills of strategic planning and reasoning as well as ideas of analogy and, through this, generalising. Students at all levels of ability and age can access them. At the most basic level, they offer opportunities for practising
arithmetical skills. At a higher level, they can be used to promote mathematical discussion by demanding detailed and reasoned explanations for a winning strategy, or an explanation of the mathematics that links the games. Once pupils identify generalisations by introducing some variables (number of counters to start with and number of counters that can be removed) further variables can be
explored and new generalisations will emerge such as the number of piles.
Make a pile of seven counters. Two players each take turns to remove either one or two counters from the pile. The player who takes the last counter is the winner.
Play the game several times to begin searching for winning strategies. Ask whether it matters who goes first and encourage pupils to record their moves. Encourage opponents to become partners in investigation as they test their theories. The aim for each player is not to win but to find out how to win. To do this, it is often worth trying ideas out by suggesting that each pupil play a
particular role (always taking two counters, for instance).
In the classroom the teacher's role is critical. Getting pupils to try out and test ideas without leading them along a particular path is an important skill. Ways to help with this include listening in on pupils' conversations and spending time with the class listing some of their conjectures on the board. Establishing some of the theories pupils have been working on helps them identify what
they have noticed so far. Another approach is to use a "conjecture board" and ask pupils to write their hypotheses on it as they work. Pupils come to see the board as their own tool for thinking aloud and sharing ideas. A nudge from you to a group that has a good idea will result in a conjecture appearing on the board.
Encourage pupils to explain and justify their strategies and suggest that they try to convince others of its validity. Then, once a strategy has been identified, it is time for a "What if?" question.
- What happens if you start the game with a different number of counters? (A series of key numbers will emerge, as well as some interesting observations about odds and evens and multiples).
- What if you can take a different number of counters away?
- What if the player to remove the last counter(s) is the loser?
Make a row of 3 counters, a row of 4 and a row of 5. Two players each take turns to remove any number of counters from a particular row. The player left with the last counter is the loser (or winner, as agreed at the start).

Place a counter on each of the four coloured squares. Two players take turns to move any counter one, two or three spaces, until they reach the end of the track and are removed. No jumping is allowed. The winner (or loser as agreed) is the person left with sliding the last counter of the track.

This is a game for two players. You will need a game board and four counters (or coins). If you are drawing it yourself, count the spots carefully. Place a counter on each star. Players take turns to move any counter, moving out towards the snail's tail. A counter can only be moved by sliding it ahead 1, 2 or 3 spots. Counters cannot jump on or pass each other.
When a counter reaches the tail, it slides of and is out of the game. The winner is the player who slides the last counter off the snail.
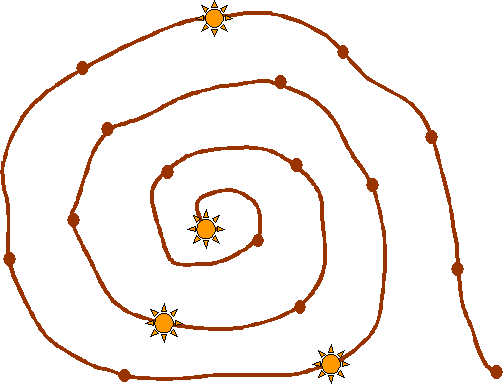
Does it matter who goes first? What happens if there are more or less spots to start with? Does it matter if the stars are in different places? Make up your own Slippery Snail game. What is the connection between this and NIM?
Links to the Framework
The following objectives are to be found in the Frameworks for teaching mathematics for Key Stages 1, 2 and 3, and apply to the activities in this theme.
- Solve mathematical problems or puzzles, recognise simple patterns and relationships, generalise and predict.
- Understand addition and subtraction mental calculation strategies.
- Use letter symbols to represent unknown numbers or variables.
- Represent problems mathematically.
- Explain and justify methods and conclusions.
- Use logical argument to establish the truth of a statement.
- Solve increasingly demanding problems and evaluate solutions.
- Present a concise, reasoned argument, using symbols, diagrams, graphs and related explanatory text.
- Suggest extensions to problems, conjecture and generalise.
And finally
Having mastered some of the fine detail concerning the strategies associated with some of these games the next step is to encourage pupils to think of Nim like games of their own.
This article is based on a number of articles on the NRICH site produced by NRICH team members. For more information search for "games" on the NRICH website.
References
- Aldridge, S. and Badham, V. (1993). "Beyond just a game". Pamphlet Number 21 . Primary Mathematics Association.
- Davies, B. (1995). "The role of games in mathematics". Square One . Vol.5. No. 2
- Gough, J. (1999). "Playing mathematical games: When is a game not a game?" Australian Primary Mathematics Classroom . Vol 4. No.2
- Oldfield, B. (1991). "Games in the learning of mathematics." Mathematics in Schools . January

