Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011 Revised 2019
What's Inside/outside/under the Box?
Shape and space offers wonderful opportunities for enriching children's experiences in mathematics in practical ways, as well as making links with other areas of the curriculum, such as art, religious education and history. If it is simply reduced to making tables about the properties of different kinds of triangles and quadrilaterals then we are missing plenty of mathematical treats.
At Key Stage 1, some of the initial ideas are related to descriptions of position and shape, and children need to be exposed to plenty of activities that enrich their use of language. Vocabulary such as "over", "under", "below", "above", "before", "after", "inside", "outside", "round", "square", "straight", "curved", and so on, is all-important. One activity that I enjoy using with young children
is attribute tables that ask children to place objects in the places that match the headings of the rows and the columns. It is important to start off with practical equipment such as Compare Bears and to encourage children to talk about the problems by working in pairs. Once children have had plenty of practical experiences with arranging concrete objects on grids, they should be ready to tackle
something slightly more abstract such as:
What Shape and Colour :

Fill in the empty boxes.
That problem is based on the vocabulary describing shape and colour.
Coloured squares builds on this but adds in vocabulary about position too:

Use these clues to colour each shape:
- Blue is between green and red
- Orange is below green
- Yellow is to the left of both purple and orange.
- What shape can you make if everyone makes a corner?
- Can you make one with all the sides the same length?
- How many lines of symmetry does it have?
- With all four of you holding part of the string, make a quadrilateral that has one line of symmetry.
- How could you convince someone else watching that your shape has just one line of symmetry?
- Now use the string to form a quadrilateral with two lines of symmetry.
- Again, how could you prove where these two lines lie?
- Now use the string to form a quadrilateral with three lines of symmetry.
- Is it possible? Explain.
- Now use the string to form a quadrilateral with four lines of symmetry.
- Where do the four lines lie?
- Each of the six diamond-shaped points is a vertex shared by two squares.
- The other 28 points are each a vertex of just one square. All of the squares share at least one vertex with another square.
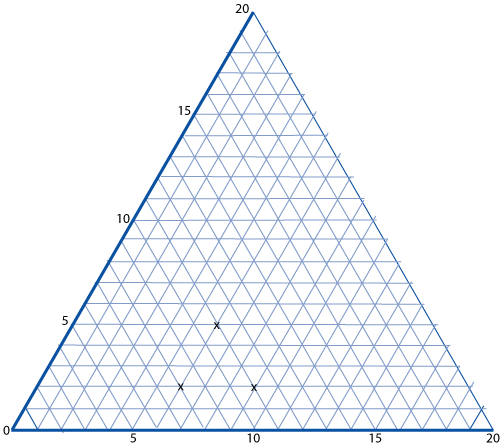
The marked points are (6, 2), (6, 5) and (9, 2). When joined they form an equilateral triangle.
The following five sets of points are also triangles.
A. (1, 13), (6, 8) and (6, 13).
B. (1, 1), (3, 3) and (7, 1).
C. (12, 1), (17, 1) and (8, 9).
D. (1, 10), (5, 2) and (6, 6).
E. (7, 5), (15, 4) and (7, 11).
What kinds of triangles are they?
Can you work out any of the angles at the vertices?
The final question will be quite a challenge for children at upper Key Stage 2 with some of the angles rather tricky to calculate. There are a few that are straightforward and can be easily worked out using the properties of isosceles, equilateral and right-angled triangles as well as the 60-degree angles in the isometric grid.
The next question would be best tackled using lots of straws or rods of different lengths. It would be best to scale the sizes up so that the rods were easy to handle, making them possibly 9cm, 12cm and 15cm long.
Triangle Edges
You have lots of sticks of 3, 4,and 5 units long. How many triangles can you make using these sticks? Each side can only use one stick but a triangle can use more than one stick of the same length. A further question would be to ask "How do you know you have them all?" This leads on to the idea of proof.
So far I have only looked at problems involving shape in two-dimensional space. Three dimensions open up a whole new range of possibilities. I can remember being told by someone that geometry should be tackled with very young children in three dimensions first of all because that is our normal environment. Certainly the language of position that I referred to earlier does make a good introduction
to work in three dimensions as well as two. Now let us consider a few questions that take children into three dimensions. In three dimensions practical apparatus becomes even more essential in order to help children to visualise the mathematical attributes of the shapes they are considering.
Sponge Sections
You have been given three shapes made out of sponge; a sphere, a cylinder and a cone:
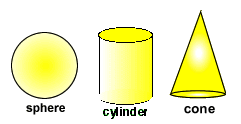
- You are going to make some shapes for printing out of these sponges.
- How would you cut the sphere to make the largest circle for printing?
- How could you make the largest possible circle from the cylinder? And the cone?
- Which shape would you use to make a very small circle for printing?
- If you cut the shapes in different ways, what other shapes for printing could you make?
- If you make two cuts, are other shapes possible?