The Mean Problem

There are four unknown numbers. The mean of the first two numbers is 4, and the mean of the first three numbers is 9. The mean of all four numbers is 15. If one of the four numbers was 2, what were the others?

Alphabetti Sudoku

Stage: 3 and 4 Challenge Level:

By Henry Kwok

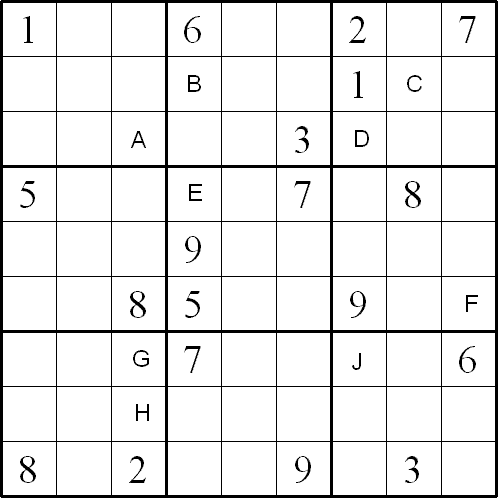
Rules of "Alphabetti Sudoku"

Like the standard sudoku, this sudoku variant consists of a grid of nine rows and nine columns subdivided into nine 3x3 subgrids.
It has two basic rules:

Each column, each row, and each box (3x3 subgrid) must have the numbers 1 through 9
No column, row or box can have two squares with the same number.

The puzzle can be solved with the help of some starting digits and 9 upper-case letters in certain squares.
The 9 upper-case letters (J and A to H) stand for the 9 mathematical problems given below.
Find the digit in each box of the given problems. After that, you will have to substitute all the letters with the answers and solve the sudoku puzzle with the usual strategy and techniques.

Below are the nine problems. Can you find the answer in each of the problems?

$A. \; 631 - 2\bigcirc 9 = 372$

$B. \; 5\bigcirc 4 + 584 = 1128$

$C. \; 318 \times 6\bigcirc 3 = 220374$

$D. \; 140781 \div 1\bigcirc 7 = 843 $

$E. \; 13\bigcirc :209 = 7:11 $

$F. \; 32\%$ of $7\bigcirc 1 = 230.72$

$G. \; \frac{\bigcirc 2}{45} \times \frac{5}{4} = \frac{1}{3}$

$H. \; \frac{3}{5} - \frac{\bigcirc}{12} = \frac{1}{60}$

$J. \; $The average of $98$ and $\bigcirc 6$ is $92.$

Mathematical reasoning & proof. Networks/Graph Theory. Working systematically. Combinatorics. Logo. Number operations - generally. Factors and multiples. Simultaneous equations. Inverses. Visualising.

You may also like

The Mean Problem

Alphabetti Sudoku

Stage: 3 and 4 Challenge Level:

Rules of "Alphabetti Sudoku"