Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Two Regular Polygons
Age 14 to 16
Challenge Level 





Two polygons fit together so that the exterior (orange) angle at
each end of their shared side is $81^\circ$.
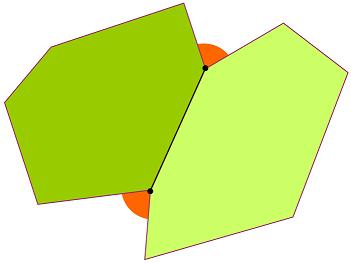
If both shapes now have to be regular polygons, but do not need to be the same, and each polygon can have any number of sides, could the orange angle still be $81^\circ$, and if that is possible how many sides would each polygon have?
Find solutions for when the orange angle is $27^\circ$ and when it is $54^\circ$.
Can you make a conjecture about the connection between the size of the orange angle and the number of sides on each polygon.
If you can, are you able to justify your conjecture?
If both shapes now have to be regular polygons, but do not need to be the same, and each polygon can have any number of sides, could the orange angle still be $81^\circ$, and if that is possible how many sides would each polygon have?
Find solutions for when the orange angle is $27^\circ$ and when it is $54^\circ$.
Can you make a conjecture about the connection between the size of the orange angle and the number of sides on each polygon.
If you can, are you able to justify your conjecture?