Ratio Sudoku 2
A Sudoku with clues as ratios.
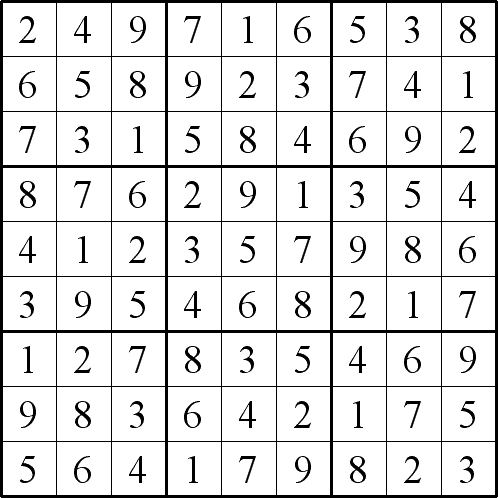
Problem
by Henry Kwok
Image

Rules for Ratio Sudoku
The small clue-numbers in this Sudoku puzzle are fractions or ratios in the lowest terms. The clue-numbers are always placed on the border lines between selected pairs of neighbouring cells of the grid. Each clue-number on a vertical border line or horizontal border line is the fraction of the two numbers in the horizontally connecting cells or vertically connecting cells respectively.
Each fraction is written in its lowest terms, with the smaller number denoted as the numerator. Thus 1/2 can stand for the following combinations of numbers in the two adjacent cells: 1 and 2, 2 and 1, 2 and 4, 4 and 2, 3 and 6, 6 and 3, 4 and 8, 8 and 4.
So if the answers in the two adjacent cells of a puzzle are actually 7 and 5, the clue-number will be written in the form 5/7 rather than 7/5, otherwise this would give away the answer and the puzzle would be too easy to solve!
The remaining rules are as in a "standard" Sudoku, and the object of the puzzle is to fill in the whole 9x9 grid with numbers from 1 to 9 (one number per cell) so that each horizontal line, each vertical line, and each of the nine 3x3 squares (outlined with the bold lines) must contain all the nine different numbers 1 to 9.
Getting Started
Caitlin kept a record of the order in which she filled the Sudoku.
She filled the cell marked 1 first, then the cell marked 2, then the cell marked 3...
You might like to retrace her route to fill in the cells in the same order, though this is just one possible route through the problem.
You can print her journey here.
Student Solutions
Image