Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Excel Investigation: Target Decimal
Age 11 to 16
Challenge Level 





What is the benefit of doing "trial and improvement" with a spreadsheet, when a calculator is often faster and more convenient?
Well firstly, I'm all in favour of calculators, and I certainly prefer quick answers to long methods.
But sometimes I need to see the things I've already tried, before I have another go, and that's where a spreadsheet helps.
So here's the puzzle:
Find a fraction a/b that is as near as possible to 0.46291
That's simple enough: 46291/100000 does it exactly.
And since 46291 and 100000 don't share any factors that's also the simplest version of the fraction.
Now try to find new a and b values, where a and b must each be less than 100.
Here's my start at this on a spreadsheet. I've put my guesses in columns A and B, and let the spreadsheet do the division.
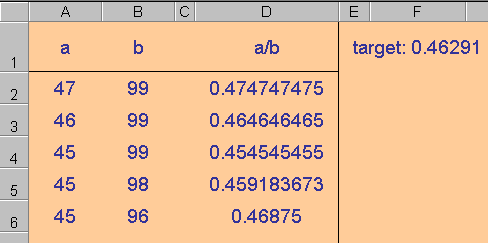
Now it's your turn. Click here to get the Target Decimal Excel file.
(Standard click-select will open the file, but to download it to your own machine: right-click on the link, and choose Save Target As . . . )
Change my choices if you like. Add three more attempts. What was your strategy?
New value
How would you explain your strategy so that someone else could use it on a new target decimal value?
Compare your approach with the strategies of other people working on the task.
Change the rules
- How about a and b values both under 40?
- What about, instead of division, multiplying a and b to get as near as possible to 789?
Scoring system
For the original a/b challenge, devise a scoring system that favours the player who:
- takes least goes
- gets closest to the target
- and uses the smallest values for a and b.
How could you decide whether your system was fair?
Compare yours with someone else's system. How do you decide which system is fairer?

