Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Excel Investigation: Power Crazy
Age 11 to 16
Challenge Level 





This month I'm exploring a puzzle called Power Crazy which appeared in June 2002.
Here's the Power Crazy puzzle:
"What can you say about the values of n that make 7n + 3n a multiple of 10?"
and
"Are there other pairs of integers between 1 and 10 which have similar properties?"
We might begin by using Excel to get some results for 7n + 3n , for integer values of n from 1 upwards, and see which of these are multiples of 10. The Excel file Power Crazy.xls shows this: right-click on the link, choose "Save Target As", and select where you want the file to be saved.
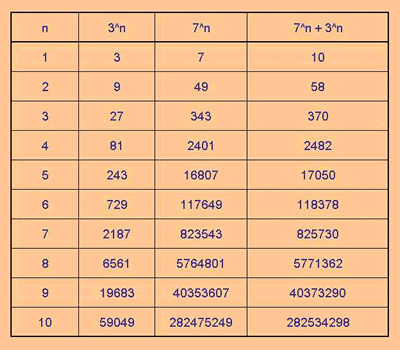
Notice that the spreadsheet doesn't solve the problem, it just does the calculation! In fact, no spreadsheet, however many results it shows, can be a replacement for the reasoning process.
So what pattern do you see? And (key question) why does it occur?
Can we now answer the first part of the puzzle: "What can you say about the values of n that make 7n + 3n a multiple of 10?"
And how about the second part to the puzzle: "Are there other pairs of integers between 1 and 10 which have similar properties?"
It does seem possible that there may be a connection between the two base numbers in the calculation and the multiple being considered; between the 3, 7, and 10.
So what about other combinations?
Suppose we allowed the base numbers to vary, and showed the results as a table.
Download the Excel file Power Crazy 2.xls .
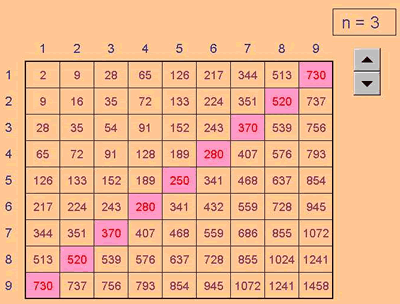
Excel has done the calculation for us (after we told it what we wanted done), but it has not explained why anything happens (or doesn't happen). That's our job!
Look at what produced multiples of 10. One arrangement group which includes the 3-7 combination, looks very promising. It is the group, 1-9, 2-8, 3-7, 4-6, and 5-5, which all work provided we use only odd values of n.
It would be nice to generalise and prove something here.
The next bit depends on how much algebra you want to do, but you can take a big leap forward in understanding what's going on if you look at xn + (10-x)n .
For example if x is 3, then (10 - x) would be 7, and we have the original puzzle.
So by using algebra we can analyse the general situation, not just the 3-7 combination. x is the variable allowing us to represent the whole group.
Here's what to do:
Look at xn + (10-x)n for the case when n = 2: x2 + (10-x)2 can be re-written as 100 - 20x + 2x2 , because (10 - x)2 is the same as 100 - 20x + x2 .
This doesn't help very much, but the next n value is more interesting: xn + (10-x)n for the case when n = 3:
That's x3 + (10-x)3 , and can be re-written as 1000 - 300x + 30x2 , because (10 - x)3 is the same as 1000 - 300x + 30x2 - x3 and the final term - x3 exactly cancels out x3 the first term of the whole x3 + (10-x)3 expression.
The terms that then remain will all have a factor of 10, and so the whole expression must be a multiple of 10.
Continuing the algebra for the cases when n = 5, or 7, or 9, and so on, there will always be a final term to exactly cancel out the first term, and all other terms will have a factor of 10.
So what have we explained?
That for all odd n, xn + (10-x)n will always be a multiple of 10.
Some questions to extend the idea:
Would odd values of n make 5n + 3n a
multiple of 8 and so on?
Here's an Excel file that let's you change the value of the
multiple being picked out with conditional formatting: Power Crazy 3.xls .
And what about those combinations which produced multiples of
10 using values of n that were not odd?
For example: 62 + 82 or 72 +
92
Final thought:
However much of the algebra you use and follow, the purpose of
this web page is to illustrate how a spreadsheet can be created to
give us numbers, and leave our brains free to think about what we
see and why it happens. And like any tool, it takes practice!

