Simplifying transformations
How many different transformations can you find made up from
combinations of R, S and their inverses? Can you be sure that you
have found them all?
Problem
This problem follows on from Combining Transformations .
We shall concentrate on the transformations $I$, $R$ and $S$ in this question. Here they are again:
Image
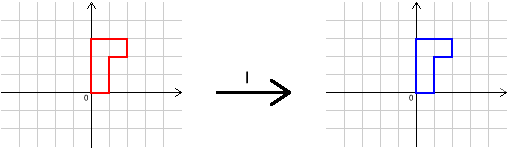
Image
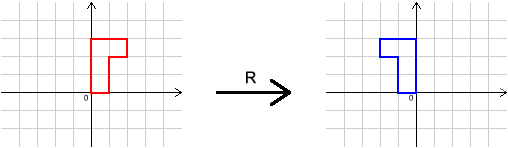
Image
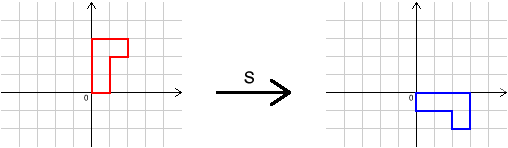
We can combine $R$, $S$, $R^{-1}$ and $S^{-1}$ in lots of different ways.
$S S R S R^{-1} S R S R^{-1}$ and $ S^{-1} R R S R S R R^{-1} S R^{-1}$ are two examples of transformations obtained like this.
In fact, there are infinitely many ways to combine them.
How many different transformations can you find made up from combinations of $R$, $S$ and their inverses?
(We shall count two transformations as the same if they have the same effect on all starting shapes.)
Can you be sure that you have found them all?
Convince yourself that $R S = S^3 R$.
In Combining Transformations you found simpler expressions for powers of $R$ and $S$.
Use these and $R S = S^3 R$ to simplify $S S R S R^{-1} S R S R^{-1}$ and $S^{-1}R R S R S R R^{-1} S R^{-1}$.
You might like to look at the article Grouping
Transformations , which explains some of the mathematics behind
these problems.
Getting Started
This is a hint to help you show that you've found all of the different transformations:
Once you think you've found them all, try drawing the upside-down `L' shape on a piece of squared paper, and draw the effects of all of the different transformations on that shape on the same piece of squared paper.
What happens if you apply $R$ or $S$ to one of the shapes now? How does this help you?
If you need some squared paper you can download it here.
Student Solutions
Jannis Ahlers (Long Bay Primary) found 8 transformations:
"The answer is 8. I found this by finding all the possible positions the shape could end in by only using R, S and there inverses."
The 8 possible transformations are:
$I$, $S$, $S^2$, $S^3=S^{-1}$, $R$, $R S=S^{-1}R$, $R S^2=S^2R$, $ R S^3=S R$.
There are eight transformations made up only of $R$, $S$ and their inverses. Neat way to see this: draw the eight that you think exist, then note that applying $R$ or $S$ to any of them gives another of them, so we can't `escape' from these eight. The simplest expressions for the eight are:
$I$, $S$, $S^2$, $S^3=S^{-1}$, $R$, $R S=S^{-1}R$, $R S^2=S^2R$, $ R S^3=S R$.
Notice that $R S R^{-1}=S^{-1}$. (Of course, $R^{-1}=R$, so $R S R=S^{-1}$, and this can also be written as $S R=R S^{-1}$.)
So the two expressions simplified are:
$S S R S R^{-1} S R S R^{-1} = S S(R S R^{-1})S(R S R^{-1})= S S S^{-1}S S^{-1} = S$
and
$S^{-1}R R S R S R R^{-1} S R^{-1} = S^{-1}(R R)S R S(R R^{-1})S R^{-1} = S^{-1} S R S S R^{-1}=(S^{-1}S)R S S R^{-1}=R S(S R)=R S R S^{-1}= (R S R)S^{-1}=S^{-1}S^{-1}=S^{-2}=S^2$.
Teachers' Resources
This problem is the third of three related problems.
The first two problems are Decoding Transformations and Combining Transformations .
There is also an article about the mathematics underlying these problems, called Grouping Transformations .
We have adopted the convention of listing a sequence of transformations from left to right; teachers may want to mention to their students that in other contexts a sequence of transformations may be listed from right to left.
